ОБОРУДОВАНИЕ: Штангенциркуль, микрометр, тела цилиндрической формы.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Измерение линейных размеров.
1. Для измерения линейных размеров и угловых величин используют различные приборы и инструменты. Наиболее простым из них является масштабная линейка. Величина наименьшего деления такой линейки, выраженная в мм, называется ценой деления.
Если измерение длин необходимо провести с большой точностью, то применяют вспомогательную шкалу измерительного инструмента-нониус.
Нониус бывает линейный (у штангенциркуля)-для измерения линейных величин, и угловой (у угломера)-для измерения угловых величин.
2. Штангенциркуль (рис.1.1.2) служит для линейных измерений, не требующих высокой точности. Он состоит из стальной штанги А (с неподвижной ножкой В) со шкалой, цена деления которой обычно равна 1 мм. Вторая ножка Д подвижная, имеет нониус С.
Нониусом называется специальная шкала, дополняющая обычный масштаб и позволяющая повысить точность измерения в 10-20_раз.
Линейный нониус представляет собой небольшую линейку С, скользящую вдоль основной шкалы. Когда ножки В и Д соприкасаются, нуль нониуса и основной шкалы совпадают (рис, 1.1.1).
Нониусы изготавливаются таким образом, чтобы длина всех делений нониуса была равной (Kn-1) делений шкалы штанги А, где К-целое число [обычно равно 2 (рис.1.1.1. и 1.1.2.) или 5].
Если a -цена деления нониуса (определяется как отношение длины нониуса по основной шкале А в мм. к числу делений нониуса n), b. - цена деления масштабной шкалы А, то связь между делениями основной шкалы и нониуса следующая:
na=(kn-1)b 1.1.1
Получаемая из этого выражения разность
kb-a=b/n 1.1.2
называется точностью нониуса.
Точность нониуса равна отношению цены деления масштабной шкалы к числу делений на нониусе.
Для нашего примера (рис. 1.1.2.) n=10; К=2;b=1мм.
Цена деления нониуса:
(kn-1)b/n=(k-1/n)b=1,9мм.
точность нониуса:
kb-a=2*1-1,9=0,1мм.
b/n=1/10=0,1мм.
Чтобы измерить длину предмета, его помещают между ножками штангенциркуля В и Д, которые сдвигают до соприкосновения с предметом и закрепляют винтом Е. (рис.1.1.2.). После этого делают отсчет по линейке и нониусу и вычисляют длину предмета.
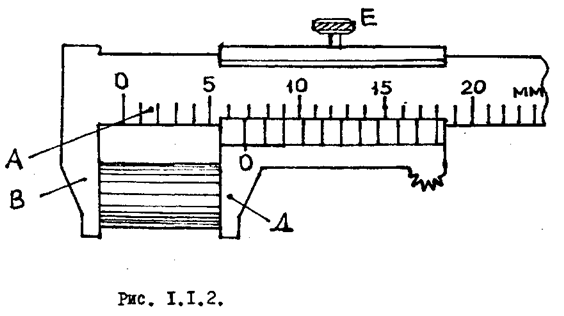
Для этого отсчитывают целое число миллиметров по линейке А , укладывающееся до нулевого деления нониуса. Затем по нониусу находят какое по счету деление нониуса совпадает с делением линейной шкалы, умножают на точность нониуса и прибавляют к показаниям линейки.
Для рис.1.1.2. находим: отсчет по линейке 6...мм, отсчет по нониусу-(совпадает 2-е деление нониуса с делением по основной шкале) 0,2 мм. Таким образом, длина предмета 6,2 мм.
При однократном или многократных измерениях в качестве систематической ошибки следует брать величину равную точности нониуса.
3. Микрометр служит для более точных измерений линейных размеров. Основной частью его является микрометрический винт (рис.1.1.3а) работа которого заключается в том, что линейное перемещение винта прямопропорционально величине его шага и углу поворота:
L=hφ/2π
Где:
L-линейное перемещение винта,
φ-угол поворота винта в радианах,
h-шаг винта - смещение барабана вдоль линейной шкалы за 1 оборот.
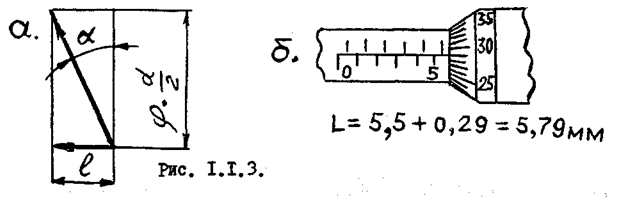
Из рис. 1.1.З а видно, что при движении точки А по винтовой линии с небольшим углом подъема α , малые перемещения L в осевом направлении легче и точнее можно измерить, отсчитывая их угловое перемещение. С этой целью на окружности барабана нанесено 50 делений, позволяющие отсчитывать малые линейные перемещения винта. Для измерения числа целых оборотов служит линейная шкала.
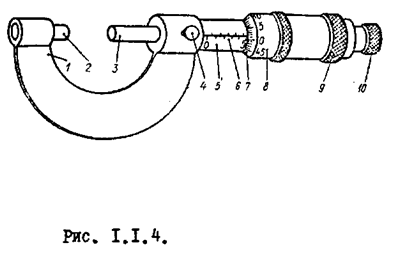
Микрометр состоит из скобы 1, на которой крепятся основные детали, неподвижной пятки 2, вращающегося шпинделя 3 с микровинтом, стопорного винта 4 для закрепления шпинделя, гильзы 5 с линейкой (основной) шкалой 6, барабана 8 с круговой шкалой 7, колпачка 9 для крепления барабана на шпинделе и трещетки 10, служащей для равномерного нажатия шпинделя на измеряемый образец. (Рис.1.1.4.). Линейная шкала 6 на гильзе 5, деления которой нанесены через 1 мм. представляет из себя две шкалы, сдвинутые друг относительно друга на 0,5 мм(см.рис.1.1.3 б).
Измерения с помощью микрометра производятся в следующем порядке. Предмет помещают между пяткой 2 и шпинделем 3 и, вращая барабан при помощи трещотки 10, доводят шпиндель до упора о поверхность предмета, сигналом чего служат щелчки трещотки. По линейной шкале, против скошенного края барабана, отсчитывают целое число делений с точностью до 0,5 мм. Десятые и сотые доли миллиметра отсчитывают по делению круговой шкалы» оказавшемуся против горизонтальной линии основной шкалы, как это было указано на рисунке 1.1.3 б.
Так как с помощью микрометра можно измерять с точностью до 0,01 мм., то в качестве погрешности, при однократном измерении, принимают половину этой величины, т.е. ± 0,005 мм.
Для измерения высоты используют штангенциркуль, диаметра-микрометр, массы-технические весы.
Так как высота и диаметр могут оказаться неодинаковыми в разных местах (дефект обработки), то измерение следует проводить не менее 5 раз в разных точках и в разных направлениях. Высоту следует измерять не по центру оснований, а по их краям, так как возможна их не параллельность. Результаты следует заносить в таблицы Расчеты погрешностей следует вести по статистическим методам обработки результатов измерений.
ВОПРОСЫ К ДОПУСКУ
1. Что представляет собой нониус?
2. Как производится отчет размера предмета с помощью нониуса?
3. Каково устройство штангенциркуля?
4. Каково устройство микрометра?
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каким прибором следует воспользоваться, если один и тот же линейный размер тела можно измерить штангенциркулем и микрометром?
2. Выведите формулу линейного нониуса.
3. В каких измерениях данной работы учитывалась систематическая ошибка? Как вы её учитывали?
4. Какая из ошибок: систематическая или случайная преобладала при измерениях? В каких случаях достаточно ограничиться одной, и в каких необходимо учитывать обе?
5. Как учитывалась приборная погрешность при оценке погрешности результата?
Внимание выполнение работы и ход работы находится внутри файла.
