cov(X,Y)=M[(X-MX)(Y-MY)]=M[XY-XMY-YMX+MX•MY]=MXY-2MX•MY+MX•MY=MXY-MX•MY

Если случайные величины XY независимы, то их коэффициент ковариации равен нулю, обратное в общем случае неверно.

Коэффициентом корреляции случайных величин X и Y называется число:

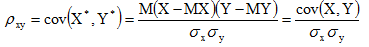
X*=(X-MX)/σ_x
Y*=(Y-MY)/σ_y

D(X±Y)=M[X±Y-M(X±Y)]²=M[X±Y-MX∓MY]²=M[(X-MX)±(Y-MY)]²=M[(M-MX)²±2(X-MX)(Y-MY)+(Y-MY)²]=M(X_MX)²±2M(X-MX)(Y-MY)+M(Y-MY)²=DX±cov(XY)+DY

Следствие:

Если X и Y независимы, то коэффициент ковариации равен 0 и следовательно

Свойства коэффициента корреляции

1. -1≤p_xy≤1
2. Если |p_xy|=1, то с вероятность 1 X и Y связаны линейно.
То есть, если коэффициент корреляции |p_xy|=1, то результаты опыта лежат на прямой

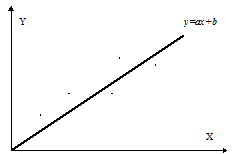
В общем случае Y можно представить в виде

Коэффициент корреляции является мерой близости линейной связи между случайными величинами X и Y: чем ближе коэффициент корреляции по модулю к 1, тем более тесно результаты конкретного испытания над X и Y соотносятся с прямой ax+b.