где р(х) и q(х) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка. Название уравнения объясняется тем, что неизвестная функция у и ее производная у' входят в уравнение линейно, т. е. в первой степени.
ОПРЕДЕЛЕНИЕ. Если q(х) = 0, то уравнение (10) называется линейным однородным уравнением. Если q(х)≠0, то уравнение (10) называется линейным неоднородным уравнением.
Для нахождения общего решения уравнения (10) может быть применен метод вариации постоянной. В этом методе сначала находят общее решение линейного однородного уравнения:
соответствующего данному неоднородному уравнению (10). Уравнение (11) является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, имеем:
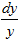 =-p(x)dx ⇒ ln|y|=-∫p(x)dx+ln|C1|
=-p(x)dx ⇒ ln|y|=-∫p(x)dx+ln|C1|
Отсюда, потенцируя, находим общее решение данного уравнения:
где С=±C1 — произвольная постоянная.
Теперь найдем общее решение уравнения (10) в виде (12), где С будем считать не постоянной, а новой неизвестной функцией от х (в этом смысл метода!), т. е. в виде
Чтобы найти функцию С(х) подставим решение в виде (13) в уравнение (10). Получим:
C'(x)e-∫p(x)dx-C(x)p(x)e-∫p(x)dx+p(x)C(x)e-∫p(x)dx=q(x) (14)
или
C'(x)=q(x)e∫p(x)dx (14')
Итак, чтобы функция (13) являлась решением уравнения (10), функция С(х) должна удовлетворять уравнению (14). Интегрируя его, находим:
C(x)=q(x)e∫p(x)dxdx+C1
где C1 — произвольная постоянная. Подставляя найденное выражение для С (х) в соотношение (10), получаем общее решение линейного уравнения (10):
y(x)=C1e-∫p(x)dx+e-∫p(x)dx∫q(x)e∫p(x)dxdx
Пример 7. Найти общее решение уравнения у'+Зу=е2х.
Данное уравнение является линейным. Здесь р(х)=3, q(х)=е2х. Решаем сначала соответствующее однородное уравнение y'+3y=0. Разделяя переменные 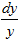 =-3dx и интегрируя, находим ln|y|=-3x+ln|C1| или y=±C1e-3x=Ce-3x. Ищем общее решение данного уравнения в виде y=C(x)e-3x. Дифференцируя, имеем y'=C'(x)e-3x-3C(x)e-3x. Подставляя в данное уравнение выражения для у и у', получаем C'(x)e-3x=e2x, C'(x)=e5x или dC=e5xdx, откуда C(x)=
=-3dx и интегрируя, находим ln|y|=-3x+ln|C1| или y=±C1e-3x=Ce-3x. Ищем общее решение данного уравнения в виде y=C(x)e-3x. Дифференцируя, имеем y'=C'(x)e-3x-3C(x)e-3x. Подставляя в данное уравнение выражения для у и у', получаем C'(x)e-3x=e2x, C'(x)=e5x или dC=e5xdx, откуда C(x)=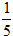 e5x+C2, где C2 - произвольная постоянная. Следовательно, общее решение данного уравнения имеет вид:
e5x+C2, где C2 - произвольная постоянная. Следовательно, общее решение данного уравнения имеет вид:
y=C(x)e-3x=(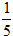 e5x+C2)e-3x или y=
e5x+C2)e-3x или y=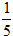 e2x+C2e-3x
e2x+C2e-3x
Метод И. Бернулли
Суть заключается в следующем. Решение уравнения (10) ищется в виде произведения двух других функций, т.е. с помощью постановки (подстановка Бернулли):
y=u(x)+v(x)
где u(x), v(x) - неизвестные функции от x, причем одна из них произвольна. Тогда y'=u'v+uv' Подставляя выражения для y и y' в уравнение (10), получаем:
Выберем функцию v(x) так, чтобы сумма в скобках обратилась в нуль, т.е. v'+p(x)v=0. Итак, 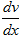 +p(x)v=0, т.е.
+p(x)v=0, т.е. 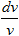 =-p(x)dx. Интегрируя, получаем: ln|v|=-∫p(x)dx+ln|c|.
=-p(x)dx. Интегрируя, получаем: ln|v|=-∫p(x)dx+ln|c|.
Ввиду свободы выбора функции v(x), можно принять c=1. Отсюда v=e-∫p(x)dx. Подставляя найденную функцию v в уравнение (10), получаем u'e-∫p(x)dx=q(x). Получено уравнение с разделяющимися переменными. Решаем его: u=∫q(x)e∫p(x)dx. Возвращаясь к переменной y, получаем решение исходного дифференциальное уравнения.
Пример 8. Найти общее решение уравнения y'+3y=e2x
Делаем замену переменных y=u•v; y'=u'v+uv', где u=u(x) - произвольная функция, v=v(x) - функция, определяемая так, чтобы y=u•v было решением уравнения u'v+uv'+3u•v=e2x. Группируем члены полученного уравнения: u'v+u(v'+3v)=e2x. Приравниваем множитель второго слагаемого, стоящий в скобках к нулю v'+3v=0; ⇒ 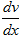 +3v=0.
+3v=0.
Решив данное дифференциальное уравнение с разделяющимися переменными, имеем
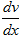 =-3v ⇒
=-3v ⇒ 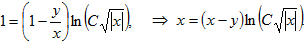 =-3dx ⇒ ∫
=-3dx ⇒ ∫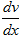 =3∫dx ⇒ ln|v|=-3x ⇒ v=e-3x
=3∫dx ⇒ ln|v|=-3x ⇒ v=e-3x
Подставляя найденную функцию v=e-3x в уравнение u'v+u(v'+3v)=e2x, найдем u
u'•e-3x=e2x ⇒ u'=e5x ⇒ 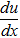 =e5x ⇒ ∫du=∫e5xdx ⇒ u=
=e5x ⇒ ∫du=∫e5xdx ⇒ u=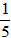 e5x+c
e5x+c
Подставляя u и v в y=u•v находим решение заданного уравнения:
y=(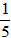 e5x+c)•e-3x или y=
e5x+c)•e-3x или y=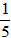 e2x+ce-3x
e2x+ce-3x
|
|
 |
zxczxc 02.06.2011 16:41 спасибо, выручили на контрольной))
|
