Материалы по теме: плотность распределения, функция распределения, дисперсия, математическое ожидание, высшая математика, лекция по высшей математике

В отличие от дискретной случайной величины непрерывные случайные величины невозможно задать в виде таблицы ее закона распределения поскольку невозможно перечислить и выписать в определенной последовательностей все ее значения. Одним из возможных способов задания непрерывной случайной величины является использование функции распределения. ОПРЕДЕЛЕНИЕ. Функцией распределения называют функцию , определяющую вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е. F(x)=P(X<x) Иногда вместо термина «Функция распределения» используют термин «Интегральная функция». Свойства функции распределения: 1. Значения функции распределения принадлежит отрезку [0;1]: 0F(x)1 2. F(x) - неубывающая функция, т.е. F(x2)F(x1), если x2>x1 Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале: P(aX<b)=F(b)-F(a) (7) Пример 9. 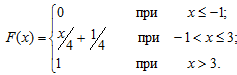Случайная величина Х задана функцией распределения: Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0;2): P(0<x<2)=F(2)-F(0) Решение: Так как на интервале (0;2) по условию, F(x)=x/4+1/4, то F(2)-F(0)=(2/4+1/4)-(0/4+1/4)=1/2. Итак, P(0<x<2)=1/2 Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю. Следствие 3. Если возможные значения случайной величины принадлежат интервалу (а;b), то: 1) F(x)=0 при xa; 2) F(x)=1 при xb. Справедливы следующие предельные соотношения: График функции распределения расположен в полосе, ограниченной прямыми у=0, у=1 (первое свойство). При возрастании х в интервале (а;b), в котором заключены все возможные значения случайной величины, график «подымается вверх». 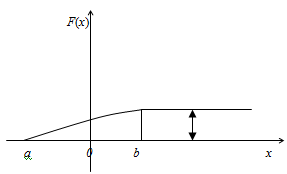При xa ординаты графика равны нулю; при xb ординаты графика равны единице: Рисунок-1 Пример 10. Дискретная случайная величина Х задана таблицей распределения: X 1 4 8 P 0.3 0.1 0.6 Найти функцию распределения и построить ее график. 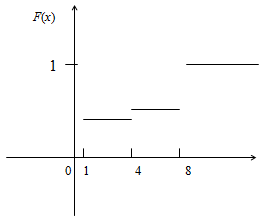Решение: Функция распределения аналитически может быть записана так: Рисунок-2 ОПРЕДЕЛЕНИЕ: Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) - первую производную от функции распределения F(x): f(x)=F'(x) Из этого определения следует, что функция распределения является первообразной для плотности распределения. Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а;b) равна определенному интегралу от плотности распределения, взятому в пределах от а до b: (8) Свойства плотности распределения вероятностей: 1. Плотность вероятностей является неотрицательной функцией: f(x)0. 2. Определенный интеграл от -∞ до +∞ от плотности распределения вероятностей непрерывной случайной величины равен 1: 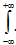f(x)dx=1. 3. Определенный интеграл от -∞ до x от плотности распределения вероятностей непрерывной случайной величины равен функции распределения этой величины: 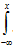f(x)dx=F(x) Пример 11. Задана плотность распределения вероятностей случайной величины Х Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5;1). Решение: Искомая вероятность: 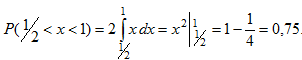Распространим определение числовых характеристик дискретных величин на величины непрерывные. Пусть непрерывная случайная величина Х задана плотностью распределения f(x). ОПРЕДЕЛЕНИЕ. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a;b], называют определенный интеграл: 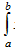M(x)=xf(x)dx (9) Если возможные значения принадлежат всей оси Ох, то: 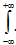M(x)=xf(x)dx (10) Модой M0(X) непрерывной случайной величины X называют то ее возможное значение, которому соответствует локальный максимум плотности распределения. Медианой Me(X) непрерывной случайной величины X называют то ее возможное значение, которое определяется равенством: P{Xe(X)}=P{X>Me(X)} ОПРЕДЕЛЕНИЕ. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [a;b], то: 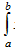D(x)=[x-M(x)]2f(x)dx (11) или D(x)=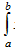x2f(x)dx-[M(x)]2 (11*) Если возможные значения принадлежат всей оси х, то: D(x)=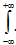[x-M(x)]2f(x)dx (12) Среднее квадратичное отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством: σ(x)=√D(x) (13) Пример 12. 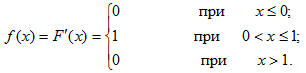Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения: Решение: Найдем плотность распределения: Найдем математическое ожидание по формуле (9): 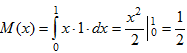Найдем дисперсию по формуле (11*): 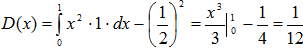Пример 13. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение непрерывной случайной величины, заданной плотностью распределения вероятностей f(x), равной 1/2 на отрезке [1,3] и 0 во всех остальных точках оси абцисс, т.е на интервалах (-∞;1) и (3;+∞). Решение. 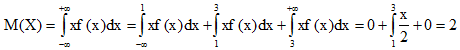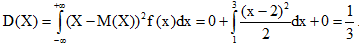Используя формулу (10), для математического ожидания и разбивая первоначальный интеграл на 3 интеграла последовательно получим: Используя формулу (11) найдем дисперсию аналогично: И по формуле (13) вычислим среднее квадратическое отклонение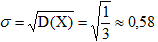

1 2 3 4 5   21.08.2010     9498     2.0/1     1     Артем   Теги: плотность распределения, функция распределения, дисперсия, математическое ожидание, высшая математика, лекция по высшей математике

Похожие статьи: Теорема сложения и теорема умножения вероятностей Случайные величины Дискретные случайные величины Двумерные дискретные случайные величины Двумерные непрерывные случайные величины Коэффициент ковариации и корреляции Вычисление и построение эмпирических функций распределения

0   1 Наталья Будённая   (17.02.2012 12:48) Я нашла опечатку: в формуле 11 со звёздочкой математическое ожидание должно быть в квадрате. Ответить

Имя *:

Код *: