Приращением функции y=f(x) называется разность y=f(x+x)-f(x),
где x - приращение аргумента x.

Если существует конечный предел отношения приращения функции y к приращению аргумента x при произвольном стремлении x к нулю, то этот предел называется производной функции y=f(x) в точке x и обозначается одним из следующих символов: y',f'(x), 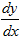. Таким образом, по определению:

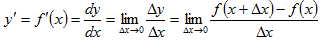
Если указанный предел существует, то функция f(x) является дифференцируемой в точке x; операция нахождения производной y' называется дифференцированием функции y=f(x).
Из равенства y/x=tgβ и определения производной следует, что производная в точке x равна тангенсу угла α наклона касательной, проведенной в точке M(x,y) к графику функции y=f(x). С физической точки зрения производная y'=f'(x) определяет скорость изменения функции в точке x относительно аргумента x, т.е. скорость есть производная пути по времени.

Если С – постоянное число и u=u(x), v=v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (C)'=0
2) (x)'=1
3) (u±v)'=u'±v'
4) (Cu)'=Cu'
5) (uv)'=u'v+uv'
6)
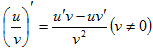
7)
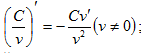
8) если y=f(u), u=φ(x) , т.е. y=f(φ(x)) - сложная функция, составленная из дифференцируемых функций, то y'_x=y'_uu'_x или 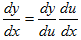; То есть производная сложной функции равна произведению ее производной по промежуточному аргументу на производную промежуточного аргумента по независимой переменой.
9) если для функции y=f(x) существует обратная дифференцируемая функция x=p(y) и 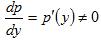, то f'(x)=1/p'(y)

На основании определения производной и правил дифференцирования можно составить таблицу производных основных элементарных функций:

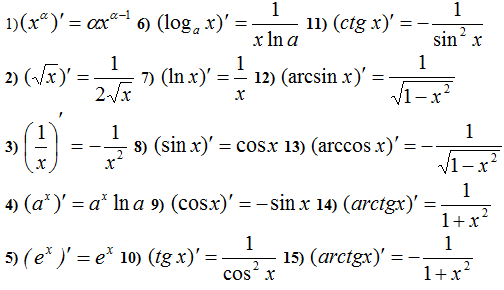
Уравнение касательной к кривой y=f(x) в точке M₀(x₀,f(x₀)) имеет вид:

Уравнение нормали (перпендикуляра) к кривой y=f(x) в точке M₀(x₀,f(x₀)):

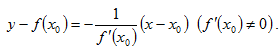
При f'(x₀)=0 уравнение нормали имеет вид x=x₀.

Углом между кривыми в точке их пересечения называют угол между касательными к кривым в этой точке.

Пример 13. Найти производную функции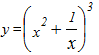

Здесь y =u³, u = x²+1/x . Значит .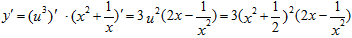

Пример 14. Найти производную функции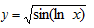

Здесь y=√t , t=sinu, u=lnx. Применив правило дифференцирования сложной функции, получим

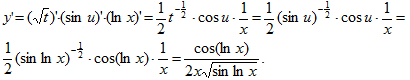
Пример 15. Найти значение производной функции y=|x| в точке x=0.

При любом приращении независимой переменной x равном x, приращение функции в точке x=0.

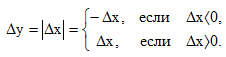
Из определения производной следует, что

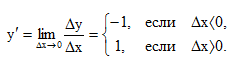
Это означает, что в точке x=0 функция y=|x| не имеет производной, хотя она и непрерывна в этой точке, поскольку .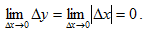

Таким образом, не всякая функция, непрерывная в некоторой точке x, дифференцируема в этой точке. Но легко показать, что любая функция непрерывна во всех точках x, в которых она дифференцируема.