Материалы по теме: закон распределения, дисперсия, математическое ожидание, высшая математика, лекция по высшей математике

Наиболее полную информацию о дискретной случайной величине дает закон распределения этой величины. ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности: X x1 x2 ... xn P p1 p2 ... pn Пример 2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тыс. тенге и десять выигрышей по 1тыс. тенге. Найти закон распределения случайных величин Х- стоимости возможного выигрыша для владельца одного лотерейного билета. Решение: Напишем возможные значения х: х1=50, х2=1, х3=0. Вероятности этих возможных значений таковы: Р1=1/100=0,01, Р2=10/100=0,1, Р3=89/100=0,89. Напишем искомый закон распределения: X 50 1 0 P 0.01 0.1 0.89 Контроль: 0,01+0,1+0,89=1. ОПРЕДЕЛЕНИЕ. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть случайная величина Х может принимать только значения х1, х2, х3,...,хn вероятности которых соответственно равны p1, p2, p3,...,pn. 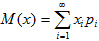Тогда математическое ожидание М(х) случайной величины Х определяется равенством: M(x)=х1p1+х2p2+...+хnpn Если дискретная случайная величина Х принимает счетное множество возможных значений, то: причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. Пример 3. Найти математическое ожидание случайной величины Х, зная закон ее распределения: X 3 5 2 P 0.1 0.6 0.3 Решение: Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности: М(х)=3 . Свойства математического ожидания 1. Математическое ожидание постоянной величины равно самой постоянной М(С)=С. 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X) 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)•M(Y). 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y)=M(X)+M(Y). Пример 4. Независимые случайные величины заданы следующими законами распределения: X 5 2 4 P 0.6 0.1 0.3 Y 7 9 P 0.8 0.2 Найти математическое ожидание случайных величин Х, Y. Решение: Найдем математическое ожидание каждой из данных величин: M(X)=5•0.6+2•0.1+4•0.3=4.4 M(Y)=7•0.8+9•0.9=9.4 Теорема. Математическое ожидание М(х) числа появлений событий А в n независимых испытаниях равно произведению этих испытаний на вероятность появления событий в каждом испытании: M(x)=np. Пусть Х- случайная величина и М(Х) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность Х-М(Х). ОПРЕДЕЛЕНИЕ. Отклонением называют разность между случайной величиной и ее математическим ожиданием. Отклонение имеет следующий закон распределения: X-M(x) X1-M(x) X2-M(x) ... Xn-M(x) P p1 p2 ... pn Теорема. Математическое ожидание отклонения равно нулю: M(X-M(x)=0). Пример 5. Задан закон распределения дискретной случайной величины Х: X 1 2 P 0.2 0.8 Доказать, что математическое ожидание отклонения равно нулю. Решение: Найдем математическое ожидание Х: M(x)=1•0.2+2•0.8=1.8 Найдем возможные значения отклонения, для чего из возможных значений Х вычтем математическое ожидание M(x):1-18=-0.8; 2-1.8=0.2 Напишем закон распределения отклонения: X-M(x) -0.8 0.2 P 0.2 0.8 Найдем математическое ожидание отклонения: M(X-M(x))=(-0.8)•0.2+0.2•0.8=0 На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. ОПРЕДЕЛЕНИЕ. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. D(x)=M[X-M(x)]2 (2) Пример 6. Найти дисперсию случайной величины Х, которая задана следующим законом распределения: X 1 2 5 P 0.3 0.5 0.2 Решение: Найдем математическое ожидание: [X1-M(x)]2=(1-2.3)2=1.69 [X2-M(x)]2=(2-2.3)2=0.09 [X3-M(x)]2=(5-2.3)2=7.29 Напишем закон распределения квадрата отклонения: [X-M(x)]2 1.69 0.09 7.29 P 0.3 0.5 0.2 По определению, D(x)=1.69•0.3+0.09•0.5+7.29•0.2=2.01 Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: D(x)=M(x2)-[M(x)]2 (3) Пример 7. Найти дисперсию случайной величины Х, которая задана следующим законом распределения: X 2 3 5 P 0.1 0.6 0.3 Решение: Найдем математическое ожидание М(х): M(x)=2•0.1+3•0.6+5•0.3=3.5 Напишем закон распределения случайной величины X2 X2 4 9 25 P 0.1 0.6 0.3 Найдем математическое ожидание M(x2): M(x2)=4•0.1+9•0.6+25•0.3=13.5 Искомая дисперсия D(x)=M(x2)-[M(x)]2=13.3-(3.5)2=1.05 Свойства дисперсии: 1. Дисперсия постоянной величины С равна нулю: D(C)=0 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. D(Cx)=C2D(x) 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. D(X1+X2+...+Xn)=D(X1)+D(X2)+...+D(Xn) 4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании D(X)=npq Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение. ОПРЕДЕЛЕНИЕ. Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии: σ(X)=√D(X) (4) Пример 8. Случайная величина Х задана законом распределения X 2 3 10 P 0.1 0.4 0.5 Найти среднее квадратичное отклонение σ(x) Решение: Найдем математическое ожидание Х: M(x)=2•0.1+3•0.4+10•0.5=6.4 Найдем математическое ожидание X2: M(x2)=22•0.1+32•0.4+102•0.5=54 Найдем дисперсию: D(x)=M(x2)=M(x2)-[M(x)]2=54-6.42=13.04 Искомое среднее квадратичное отклонение σ(X)=√D(X)=√13.04≈3.61 Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратичных отклонений этих величин: 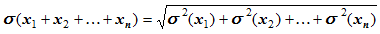(5)

1 2 3 4 5   18.08.2010     10100     4.7/3     1     Артем   Теги: закон распределения, дисперсия, математическое ожидание, высшая математика, лекция по высшей математике

Похожие статьи: Вероятность гипотез. Формулы Байеса Элементы комбинаторики Случайные величины Непрерывные случайные величины Двумерные дискретные случайные величины Статистическое распределение выборки Вычисление и построение эмпирических функций распределения

0   1 Ирина   (07.02.2011 21:07) Спасибо огромное, очень помогли. Ответить

Имя *:

Код *: