Двумерная случайная величина называется непрерывной случайной величиной, если пространством ее элементарных событий является плоскость, либо область плоскости. Очевидно что X и Y являются одномерными непрерывными случайными величинами.

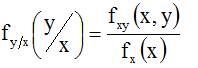
Числовая скалярная функция двух действительных аргументов называется двумерной плотностью вероятности двумерной случайной величины XY, если для фиксированных значений своих аргументов выполняется равенство .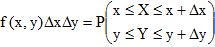

Приведенное здесь определение является аналогичным определению одномерной плотности вероятности.

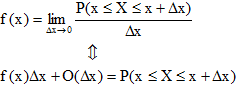
Числовая скалярная функция двух действительных аргументов называется двумерной функцией распределения, если она при фиксированном числе своих аргументов численно равна вероятности наступления F_x,y(x,y)=(P≤x; Y≤y), если X, У - непрерывные случайные величины, то значение функции распределения не изменится.

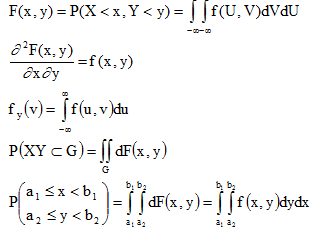
Найдем плотность вероятности случайной величины Y при условии, что в результате испытания над случайной величиной XY , X приняло значение х.

Обозначим f_y/x(y/x), P(y≤Y≤y+Δy/x=x)=f_y/x(y/x)Δy+0(Δy)

В качестве условной плотности вероятности используется следующее выражение: