Часто интерес представляет случай большого числа n и малой вероятности p успеха в одном отдельном испытании. В этом случае удобно воспользоваться приближением Пуассона.

Теорема: Если вероятность p наступления события А в каждом испытании постоянна, близка к нулю, а число независимых испытаний n достаточно велико, то вероятность P_n(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна:

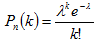, где λ=np

Эта формула называется формулой Пуассона. Обычно приближенную формулу Пуассона применяют, когда p<0,1, а npq<10.

Функция 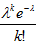затабулирована, т.е. имеет таблицу.

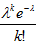
k	λ
	1	2	5	8
1	0.36	0.27	0.0337	0.0027
2	0.18	0.27	0.084	0.0107
3	0.06	0.18	0.14	0.028
4	0.0031	0.036	0.175	0.0916

Формула Пуассона используется в задачах, относящихся к редким событиям.
Пример 3. Пусть известно, что при изготовлении некоторого препарата брак (количество упаковок, не соответствующих стандарту) составляет 0,2%. Оценить приближенно вероятность того, что серди 1000 наугад выбранных упаковок окажутся три упаковки, не соответствующие стандарту.

Решение: Выбор каждой очередной упаковки можно рассматривать как независимое испытание. Из условий задачи следует, что n=1000 (т.е. велико) а p=0.002 (т.е. мало) следовательно, А можно считать редким событием. λ=np=1000•0.002=2<10
Воспользуемся приближенной формулой Пуассона или таблицей.

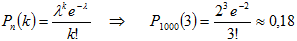
По таблице: находим ячейку пересечения стоблца λ=2 и строки k=3.