Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции:

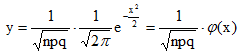
при x=(k-np)/√npq

Итак, вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна 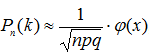, где x=(k-np)/√npq

Пример 4. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение: По условию, n=400; k=80; р=0,2, q=0,8. Воспользуемся асимптотической формулой Лапласа: 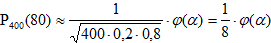. Вычислим определяемое данными задачи значение x=(k-np)/√npq=(80-400•0.2)/8=0. По таблице находим φ(0)=0.3989. Искомая вероятность P₄₀₀(80)=(1/8)•0.3989=0.04986