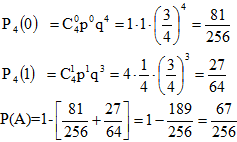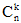 . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появление k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появление k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:
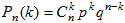 (1)
(1)или
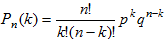 (1a)
(1a)Полученную формулу называют формулой Бернулли.
Пример 1. Вероятность того, что во время эпидемии гриппа понадобятся услуги скорой помощи на протяжении каждых 6 суток равна р=0,75. Следовательно, вероятность того, что в течение суток не будет ни одного вызова равна q=1-р=1-0,75=0,25. Найти вероятность того, что в продолжении 6 суток услуги скорой помощи понадобятся 4 суток подряд.
Искомая вероятность по формуле Бернулли равна 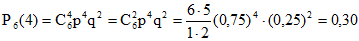
Пример 2. Студент отвечает на 4 дополнительных вопроса при сдаче экзамена. Вероятность правильного ответа на каждый вопрос будем считать равной р=1/4. Предполагая, что все ответы-события независимые, найти вероятность того, что будут даны хотя бы два правильных ответа.
Решение: А =(хотя бы два правильных ответа)-это 2, 3 или 4.
Так как р=1/4, то q=1-1/4=3/4-вероятность неправильного ответа на вопрос. Эту задачу удобно решать, используя противоположные события, т.е. пользуясь равенством:
Р(А)=1-[Р4(0)+Р4(1)]: