Допустим к ним присоединился еще один мальчик Даурен. Каковы будут способы расположения в этом случае? В возможных шести случаях Даурен может стоять первым, вторым, третьим и последним:
АДБС, АДСБ, БДАС, БДСА, СДАБ, СДБА;
АБДС, АСДБ, БАДС, БСДА, САДБ, СБДА;
АБСД, АСБД, БАСД, БСАД, САБД, СБАД.
Всего 24 разных способов. А если еще увеличить количество детей? Каждый раз писать и выводить общее количество трудно. Нам нужно определить число способов, а не виды способов. Нет ли других методов для определение этого число? - Есть. И в теории вероятностей нас больше интересует количество способов расположения, чем виды расположения. Раздел математики, называемый комбинаторикой, дает возможность сразу определить количество таких способов. Ознакомимся с основными понятиями комбинаторики, необходимыми для решения задач теории вероятностей. Это - перестановка, размещение и сочетания. Остановимся на каждом в отдельности.
1. Перестановка. Рассмотрим число случаев в предыдущей задаче. Мы переставили местами буквы А, Б, С и посчитали число всевозможных комбинаций, оно равнялось 6. А когда число мальчиков увеличилось на единицу, переставь местами буквы А, Б, С, Д, мы нашли число всевозможных комбинаций, оно равнялось 24.
ОПРЕДЕЛЕНИЕ. Перестановкой из n различных элементов называются комбинации, которые состоят из n элементов и отличаются друг от друга только порядком их расположения.
Число перестановок из n различных элементов обозначают Pn и подсчитывают по формуле:
здесь n! (читается "эн факториал") означает произведение всех натуральных чисел от 1 до n:
Понятно, что один факториал равен единице, 1! = 1, вместе с этим, в математике принято считать что и ноль факториал равен единице. И так 0! = 1.
Вернемся к примеру. Здесь n=3. Следовательно, можно найти искомое число перестановок по формуле (1): P3=3!=1•2•3=6. Аналогично, число перестановок из четырех букв равно: P4=4!=1•2•3•4=24
Пример 7. Найдем значение выражения с факториалами 8!/6!•2!
Сначала преобразуем 8!=1•2•3•4•5•6•7•8=6!•7•8
Это преобразование подставим в выражение и упростим. 8!/6!•2=6!•7•8/6!•2=7•8/2=28
2. Размещения. Рассмотрим пример. Сколько двузначных чисел (цифры не повторяются) можно записать с помощью цифр 7, 8, 9. Это можно сделать в двух этапах: первый этап - определение количество подбора разрядов десятков числа, он равен 3 (любая из данных 3 цифр может занять разряд десятков); второй этап - определение количество подбора разрядов единиц числа, он равен 2 (любая цифра из оставшихся двух может занять разряд единиц). По правилу умножения из трех чисел можно составить всего 3•2=6 различных двузначных чисел. Действительно, можно в этом убедиться непосредственно записывая эти числа 78, 79, 87, 89, 97, 98, При решении задачи мы расположили по два элемента из трех, причем эти комбинации отличаются либо составом (78, 98), либо порядком их расположения (78, 87).
ОПРЕДЕЛЕНИЕ. Размещением из n элементов по m элементов (m n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающихся друг от друга либо самими элементами, либо порядком их расположения.
n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающихся друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из n элементов по m элементов обозначают 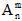 и читают так: "А из эн по эм". Чтобы найти
и читают так: "А из эн по эм". Чтобы найти 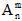 используют формулу:
используют формулу:
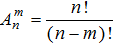 (15)
(15) В нашем примере n=3, а m=2. Тогда 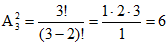
Рассмотрим еще один пример. В 5 классе изучают 10 предметов. Сколькими способами можно составить расписание, если в этот день должно быть 4 различных урока?
Чтобы найти число способов расположения 10-ти предметов по четыре предмета, воспользуемся формулой (15) нахождения числа размещений из 10 элементов по 4 элемента:
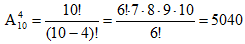
Итак, 10 предметов по 4 предмета можно расположить 5040 различными способами.
3. Сочетания. Пример. Нужно составить произведения двух различных чисел из данных трех чисел 7, 8, 9.
Учитывая переместительное свойство умножения, имеем: 7•8=56, 7•9=63, 8•9=72. При решении задачи мы отобрали по два элемента из трех, причем эти комбинации отличаются только составом (78, 98), а их расположения не влияют на произведение.
ОПРЕДЕЛЕНИЕ. Сочетанием из n элементов по m элементов (m n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающиеся друг от друга только составом.
n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающиеся друг от друга только составом.
Число сочетаний из n элементов по m элементов обозначают 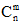 и читают так: "це из эн по эм". Чтобы найти
и читают так: "це из эн по эм". Чтобы найти 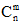 используют формулу:
используют формулу:
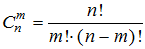 (16)
(16) В нашем примере n=3, а m=2. Тогда 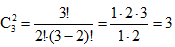
Рассмотрим еще пример. В классе 25 учеников, из них 12 мальчиков. а) Нужно составить дежурство по два человека, причем пары должны состоят либо из мальчиков, либо из девочек. б) Сколько можно создать групп для дежурства, из двух мальчиков и одной девочки?
Решение. а) При решении этой задачи воспользуемся правилом сложения и формулой сочетания. Сначала посчитаем сколько пар можно создать из мальчиков (m1) и из девочек (m2), после найдем их сумму (m=m1+m2).
Чтобы определить сколько пар можно создать из 12 мальчиков воспользуемся формулой для подсчета числа сочетаний из 12 элементов по 2 элемента
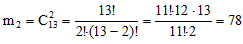
Из девочек можно создать 78 различных пар. Тогда по два мальчика и по две девочки всего можно создать m=66+78=144 различных пар.
б) При решении этой задачи воспользуемся правилом умножения и формулой сочетания. В группе два мальчика и одна девочка. Сначала посчитаем сколькими способами можно выбрать из 12 мальчиков по два мальчика (m1) и из 13 девочек одну девочку (m2), затем перемножим полученные результаты (m=m1•m2).
Из 12 мальчиков 2 мальчика можно выбрать 66 различными способами. А из 13 девочек 1 девочку можно выбрать следующим образом:
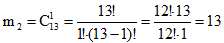
Тогда группу из двух мальчиков и из одной девочки можно создать m=66•13=856 различными способами.
