Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то событие А+В – попадание хотя бы при одном выстреле (или при первом выстреле, или при втором, или в обоих случаях).
Теорема 1.(теорема сложения вероятностей)
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Доказательство: Введем обозначения: n – общее число возможных элементарных исходов испытания; m1 – число исходов, благоприятствующих событию А; m2 – число исходов, благоприятствующих событию В.Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1+m2. Следовательно, P(A+B)=(m1+m2)/n=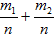 . Приняв во внимание, что m1/n=P(A) и m2/n=P(B), окончательно получим P(A+B)=P(A)+P(B)
. Приняв во внимание, что m1/n=P(A) и m2/n=P(B), окончательно получим P(A+B)=P(A)+P(B)
Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)
Пример 3. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие А) P(A)=10/30=1/3 Вероятность появления синего шара (событие В) P(B)=5/30=1/6 События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P(A+B)=P(A)+P(B)=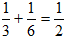
Теорема 2. Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна единице:
Доказательство: Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то:
любые два события полной группы несовместны, поэтому можно применить теорему сложения:
Сравнивая (4) и (5), получим P(A1+A2+...+An)=1
ОПРЕДЕЛЕНИЕ. Два несовместных события, образующие полную группу называются противоположными событиями. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать  .
.
Пусть в результате испытания возможны только два единственно возможных события. Например, а) при одном бросании монеты - "выпал герб" и "выпала цифра"; б) при одном бросании игральной кости - "выпало 6 очков" и "не выпало 6 очков"; с) при одном выстреле - "попадание в мишень" и "не попадание в мишень". В каждой паре событий появление одного исключает появление второго. Действительно, если монета выпала гербом, то уже не может выпасть цифрой; игральная кость не может одновременно выпасть сразу двумя гранями; стрелок попадая в мишень, исключает промах. Итак, данных примерах противоположными событиями являются: а) A={выпал герб},  ={выпала цифра}; б) B={выпало 6 очков},
={выпала цифра}; б) B={выпало 6 очков},  ={не выпало 6 очков}; с) C={попадание в мишень},
={не выпало 6 очков}; с) C={попадание в мишень},  ={не попадание в мишень}.
={не попадание в мишень}.
Теорема 3. Сумма вероятностей противоположных событий равна единице:
P(A)+P( )=1 или p+q=1, где P(A)=p, p(
)=1 или p+q=1, где P(A)=p, p( )=q
)=q
ОПРЕДЕЛЕНИЕ. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена.
ОПРЕДЕЛЕНИЕ. Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Теорема 4. (теорема умножения вероятностей) Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
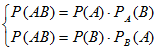 (7)
(7)Следствие 2. Эту теорему можно обобщить на любое конечное число зависимых событий A1,A2,...,Ak
P(A1,A2,...,Ak)=P(A1)•PA1(A2)•PA1A2(A3)...PA1A2...Ak-1(A)
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности PAB=P(B)
Теорема 5. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Пример 4. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В)-0,7.
Событие А и В независимые, поэтому, по теореме умножения, искомая вероятность P(AB)=P(A)•P(B)=0.7•0.8=0.56
Следствие 3. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
P(A1,A2,...,An)=P(A1)•P(A2)•...•P(An)
Теорема 5. Вероятность появления хотя бы одного из событий A1,A2,...,An, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий  1,
1, 2,...,
2,..., n
n
Доказательство: Обозначим через А событие, состоящее в появлении хотя бы одного из событий A1,A2,...,An. Событие A и  1,...,
1,..., n (ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:
n (ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:
P(A)+P( 1,
1, 2,...,
2,..., n)=1
n)=1
Отсюда, пользуясь теоремой умножения, получим:
 1,
1, 2,...,
2,..., n)=1-P(
n)=1-P( 1)P(
1)P( 2)...P(
2)...P( n)
n)или
Теорема 6. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
Доказательство: Поскольку события А и В, по условию, совместны, то событие А+В наступит, если наступит одно из следующих трех совместных событий:  B, A
B, A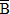 или AB. По теореме сложения вероятностей несовместных событий:
или AB. По теореме сложения вероятностей несовместных событий:
 B)+P(A
B)+P(A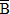 )+P(AB) (*)
)+P(AB) (*) Событие А произойдет, если наступит одно из двух несовместных событий: A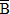 или AB. По теореме сложения вероятностей несовместных событий имеем:
или AB. По теореме сложения вероятностей несовместных событий имеем:
P(A)=P(A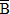 )+P(AB)
)+P(AB)
Отсюда P(A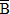 )=P(A)-P(AB)
)=P(A)-P(AB)
Аналогично имеем P(B)=P( B)+P(AB)
B)+P(AB)
Отсюда P( B)=P(B)-P(AB)
B)=P(B)-P(AB)
Подставив все в (*)б, окончательно получим P(A+B)=P(A)+P(B)-P(AB)
|
|
 |
шеравган 15.12.2010 10:46  помогите мне по 17 теория вероятности и напишите ответ помогите мне по 17 теория вероятности и напишите ответ |
