1. Статистическое дискретное распределение. Полигон.
Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 – n2 раз, хk – nk раз и ∑ni=n - объем выборки. Наблюдаемые значения х1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой ni/n=wi
ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант хi и соответствующих им частот ni или относительных частот wi.
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
| x1 | x2 | ... | xm |
| n1 | n2 | ... | nm |
(сумма всех частот равна объему выборки ∑ni=n)
или в виде таблицы распределения относительных частот:
| x1 | x2 | ... | xm |
| w1 | w2 | ... | wm |
(сумма всех относительных частот равна единице ∑wi=1)
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.
Решение. 1) Статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Напишем распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контроль: 0,1+0,2+0,4+0,1+0,2=1.
Полигоном частот называют ломаную, отрезки, которой соединяют точки (х1,n1),(х2,n2),...,(хk,nk). Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты ni. Точки (хi,ni) соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х1,w1),(х2,w2),...,(хk,wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки (хi,wi) соединяют отрезками и получают полигон относительных частот.
Пример 2. Постройте полигон частот и относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:
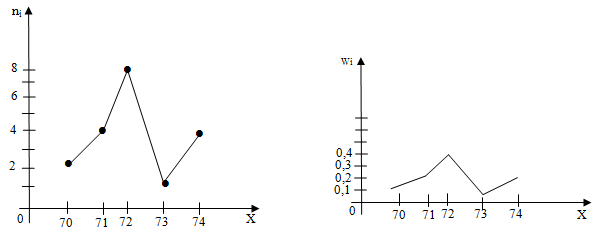
2. Статистический интервальный ряд распределения. Гистограмма. Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Замечание. Часто hi-hi-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и hi:
1. Rразмах=Xmax-Xmin
2. h=R/k; k-число групп
3. k≥1+3.321lgn (формула Стерджеса)
4. a=xmin, b=xmax
5. h=a+ih, i=0,1...k
Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
| Интервалы группировки | [h0;h1) | [h1;h2) | ... | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | ... | nk-1 | nk |
Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:
| Интервалы группировки | [h0;h1) | [h1;h2) | ... | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | ... | wk-1 | wk |
Пример 3. Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.
Решение. Определим характеристики группировки с помощью замечания.
k≥1+3.321lg50=1+3.32lg(5•10)=1+3.32(lg5+lg10)=6.6
Имеем, a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты ni | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн.частоты wi | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0 | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению wi/h (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии wi/h. Площадь i-го частичного прямоугольника равна h•wi/h=wi - относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.
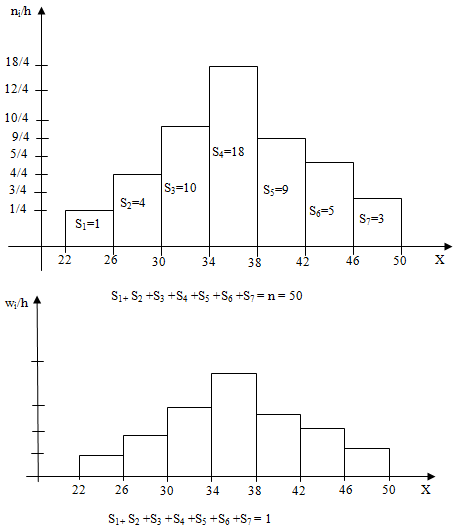
Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.
Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.
