Напишем биномиальный закон в виде таблицы:
| X | n | n-1 | ... | k | ... | 1 | 0 |
| P | pn | npn-1q | ... | Cnkpkqn-k | ... | Cm1pqn | qn |
Пример 14. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений «герба».
Решение: Вероятность появления «герба» в каждом бросании монеты p=0.5, следовательно, вероятность не появления «герба» q=1-0.5=0.5. При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения Х таковы: х1=2, х2=1, х3=0. Найдем вероятности этих возможных значений по формуле Бернулли:
P2(2)C22p2=(0.5)2=0.25
P2(1)C21pq=2•(0.5)•(0.5)=0.5
P2(0)C20q2=(0.5)2=0.25
| X | 2 | 1 | 0 |
| P | 0.25 | 0.5 | 0.25 |
Контроль: 0,25+0,5+0,25=1.
Распределение Пуассона (распределение, вероятности в котором определяются по формуле Пуассона: Pn(k)=λke-λ/k!. Выглядит таким образом:
| X | 0 | 1 | 2 | ... | k |
| P | e-λ | λe-λ/1! | λ2e-λ/2! | ... | λke-λ/k! |
Пример 15. На складе в аптеке имеется 100000 упаковок различных лекарственных препаратов. Вероятность того, что среди них имеется препарат с истекшим сроком годности равна 0,0001. Найти вероятность того, что ровно 5 упаковок не годны к применению.
Решение. По условию n=100000, p=0.0001, k=5. События состоящие в том, что препараты в 5 упаковках не годны к применению, независимы, число n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона: Pn(k)=λke-λ/k!. Найдем λ=np=10000*0.0001=10. Искомая вероятность P10000(5)=105e-10/5!=0.0375. Следовательно, закон распределения имеет вид:
| X | 0 | 1 | 2 | ... | 5 |
| P | e-10 | 10e-10/1! | 102e-10/2! | ... | 105e-10/5! |
Равномерное распределение ( распределение вероятностей непрерывной случайной величины X, у которой на интервале (a;b), которому принадлежат все возможные значения X, плотность сохраняет постоянное значение, а именно f(x)=1/(b-a), вне этого интервала f(x)=0
Пример 16. Найти математическое ожидание случайной величины X, равномерно распределенной в интервале (a;b).
Решение. График плотности равномерного распределения симметричен относительно прямой x=(a+b)/2. Поэтому M(X)=(a+b)/2. Итак математическое ожидание случайной величины, равномерно распределенной в интервале (a;b) равно полусумме концов этого интервала.
Решение. Используем формулу D(x)=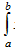 x2f(x)dx-[M(x)]2. Подставив f(x)=1/(b-a), M(X)=(a+b)/2 и выполнив элементарные выкладки, получим искомую дисперсию D(X)=(b-a)2/12. Среднее квадратическое отклонение случайной величины X равно квадратному корню из ее дисперсии σ(X)=(b-a)/2√3.
x2f(x)dx-[M(x)]2. Подставив f(x)=1/(b-a), M(X)=(a+b)/2 и выполнив элементарные выкладки, получим искомую дисперсию D(X)=(b-a)2/12. Среднее квадратическое отклонение случайной величины X равно квадратному корню из ее дисперсии σ(X)=(b-a)/2√3.
Нормальное распределение ( Непрерывная случайная величина называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет вид:
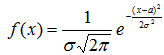 (14)
(14)где a - математическое ожидание, σ2 - дисперсия, σ - среднее квадратичное отклонение этой величины. График плотности вероятности нормального закона распределения (кривая Гаусса) приведен на рисунке 1.
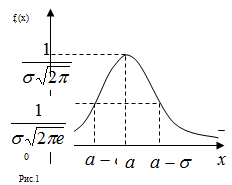
Этот график симметричен относительно вертикальной прямой x=a, причем в точке функция имеет максимум, равный 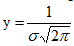 . Ось абсцисс является асимптотой графика этой функции.
. Ось абсцисс является асимптотой графика этой функции.
Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется формулой
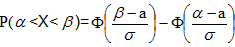 (15)
(15) где 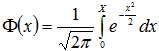 - функция Лапласа и Ф(-x)=-Ф(x) (16)
- функция Лапласа и Ф(-x)=-Ф(x) (16)
Ф(x) - табулированная функция.
Вероятность того, что абсолютная величина отклонения меньше положительного числа δ, P(|x-a|<δ)=2Ф(δ/σ). В частности, при a=0 справедливо равенство
Мода и медиана нормального распределения соответственно равны: M0=a, Me=a, где a=M(x)
Пример 18. Предполагая, случайная величина Х, определяемой как масса таблетки, наугад выбранной из некоторой партии таблеток, подчиняется нормальному распределению с математическим ожиданием a=0.5 г., и средним квадратичным отклонением σ=0.1 г., найти вероятность того, что масса наугад выбранной таблетки окажется в пределах от 0,45 до 0,55 г.
Решение: Подставив исходные данные в формулу (15), полагая при этом α=0.45, β=0.55, получим:
P(0.45<M<0.55)=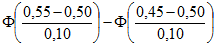 =Ф(0.5)-Ф(-0.5)=2Ф(0,5)
=Ф(0.5)-Ф(-0.5)=2Ф(0,5)
Ф(0,5)≈0.1915 (по таблице). Ввиду нечетности функции:
Ф(X), Ф(-0.5)=-Ф(0.5) ⇒ P(0.45<M<0.55)=0.3830
Распределения, связанные с нормальным распределением. В случае, когда α=0, σ=1, функция (14) принимает вид 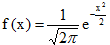 . Распределение вероятностей непрерывной случайной величины, определяемое данной формулой называется нормированным, или стандартным. График этой функции называется нормированной кривой.
. Распределение вероятностей непрерывной случайной величины, определяемое данной формулой называется нормированным, или стандартным. График этой функции называется нормированной кривой.
| Числовые характеристики | Математическое ожидание | Дисперсия | СКО | Мода. Медиана |
| Распределение | M(X) | D(X) | σx | |
| 1. Биномиальное | np | np(1-p) | √[np(1-p)] | |
| 2. Пуассона | λ | λ | √λ | |
| 3. Равномерное | (a+b)/2 | (a+b)2/12 | |b-a|/√12 | Медиана (a+b)/2 |
| 4.Нормальное (Гауссово) | a | σ2 | σ | Мода=a Mедиана=a |
