Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменилось (в связи с тем, что событие А уже наступило) вероятность гипотез. Другими словами, будем искать условные вероятности:
Найдем сначала условную вероятность PA(B1). По теореме умножения имеем:
Отсюда 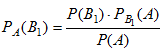 . Заменив здесь Р(А) по формуле (12), получим:
. Заменив здесь Р(А) по формуле (12), получим:
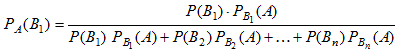
Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Bi (i=1,2,...,n) может быть вычислена по формуле:
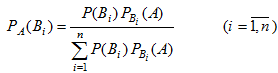 (13)
(13)Формулу (13) называют формулой Байеса (от имени английского математика, который их вывел; опубликованы в 1764). Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример 6: В группе 10 студентов, пришедших на экзамен. Трое подготовлены отлично, 4-хорошо, 2-посредственно, 1- плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный –на 16, посредственно – на 10, плохо подготовленный – на 5. Вызванный наугад студент ответил на все 3 заданных вопроса. Найти вероятность того, что этот студент подготовлен: 1) отлично 2) плохо
Решение: Рассмотрим полную группу событий: A - студент ответит на все вопросы B1 - подготовлен отлично, B2 - подготовлен хорошо, B3 - подготовлен посредственно, B4 - подготовлен плохо.
Вероятности этих событий равны: Р(B1)=0.3; Р(B2)=0.4; Р(B1)=0.2; Р(B1)=0.1
Найдем условные вероятности: PB1(A)=1; PB2(A)=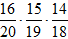 =0.491; PB3(A)=
=0.491; PB3(A)=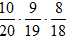 =0.105; PB4(A)=
=0.105; PB4(A)=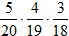 =0.009
=0.009
P(A)=0.3•1+0.491•0.4+0.105•0.2+0.009•0.1=0.518
По формуле (13) найдем
1) РA(B1)=0.3•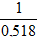 =0.58 2) РA(B1)=0.1•
=0.58 2) РA(B1)=0.1•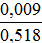 =0.002
=0.002
