1. 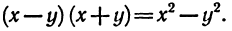
Если эту формулу записать справа налево, то получим 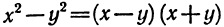 , т. е. разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
, т. е. разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
Например, 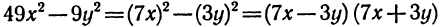
2. 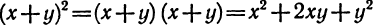 Тождество (2) называют формулой квадрата суммы. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Тождество (2) называют формулой квадрата суммы. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Например, 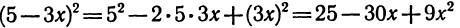
3.  Тождество (3) называют формулой квадрата разности. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Тождество (3) называют формулой квадрата разности. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
Например, 
4. 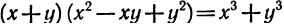 Если эту формулу записать справа налево, то, получим
Если эту формулу записать справа налево, то, получим 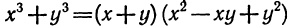 сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Примечание. Выражение напоминает нам трехчлен
, который равен квадрату разности х и у. Однако в данном выражении
вместо удвоенного произведения х и у стоит просто их произведение. Именно поэтому выражение
называют неполным квадратом разности.
Например,
5. Если эту формулу записать справа налево, то получим
, т. е. разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Например,
Выражение вида называют неполным квадратом суммы.
Приведем еще четыре формулы:
6. Тождество (6) называют кубом суммы.
7. Тождество (7) называют кубом разности.
8.
9. Тождества (8) и (9) называют квадратом трехчлена.
1. Разложить на множители:
Решение.
1) Выражение в явной форме ни одно из семи тождеств не представляет, но число 16 можно представить в виде степени с основанием 4, т. е.
. Тогда выражение
примет иной вид:
а это уже формула разности квадратов, и, применив эту формулу, получим:
2) Объединим в одну группу последние три члена, вынеся — 1 за скобки. Получим
так как можно разложить по формуле разности квадратов.
3) Это выражение в явной форме ни под одно тождество не подходит. Анализируя пример, видим, что в каждом слагаемом можно вынести общий множитель 6 за скобки. Получим:
Выражение в скобках представляет собой разложенный квадрат суммы двух выражений:
Теперь наше выражение примет вид:
4) Представим данный многочлен в виде разности кубов двух выражений и, применив формулу, получим:
Этот пример можно решить и вторым способом. Для этого представим данный многочлен в виде разности квадратов двух выражений, получим:
Теперь мы получили выражение, состоящее из двух сомножителей: разности кубов двух выражений и суммы кубов двух выражений. Первый из них разлагается на множители по формуле (5), а второй — по формуле (4):
5) Данный многочлен легко можно представить в виде суммы кубов двух выражений таким образом:
Применив формулу суммы кубов, получим:
2. Сравнить числа:
Решение.
Следовательно,
3. Найти значение выражения где
.
Решение:
4. Доказать, что при любом натуральном k значение выражения делится на 12.
Решение. Воспользовавшись формулой , упростим данное выражение:
Полученное выражение 12k делится на 12 без остатка.
5. Доказать, что значение выражения не зависит от переменной х.
Решение. Выполним указанные действия:
После преобразования данного выражения получили число 144, а это и означает, что выражение не зависит от переменной х.
