а) образовательные – продолжить формирование навыков по решению геометрических задач по теме «Равнобедренный треугольник»;

б) развивающие – вырабатывать внимание, логическое мышление, грамотную речь, интерес к предмету;

в) воспитательные – прививать аккуратность, ответственность и уважение к одноклассникам, умение слушать, отстаивать свое мнение.

Тип урока: закрепление ранее изученного материала.

Ход урока:

I. Организационный момент (1 мин). Класс делится на 4 команды – конструкторские бюро (КБ). Во главе каждого КБ стоит «главный инженер» (капитан команды), который выбирается участниками по согласованию с учителем. После постановки задачи разрешаются консультации внутри КБ для выяснения подхода к решению задачи. Консультации могут быть как групповыми, так и индивидуальными.
Учащиеся каждой команды изучают условие задачи, выполняют необходимые рисунки. Капитаны команд следят за тем, чтобы каждый ученик сделал рисунок в тетради и мог объяснить решение той или иной задачи. Через некоторое время «главные инженеры» КБ объявляют о возможности начать опрос.
К доске отвечать идут ученики по предложению «инженеров». Участники других КБ при этом могут задавать соответствующие задаче вопросы, в том числе и по теоретическому материалу. Поэтому руководитель и все члены КБ должны быть уверены за своего «сотрудника» и знать, что он их не подведет. А это, в свою очередь, требует внимательности и ответственности от каждого ученика в период подготовки и умения ответить на вопрос. Балл засчитывается тому КБ, которое первым и правильно справились с заданием. Та команда, которая набрала наибольшее количество баллов, получает в конце урока оценку в журнал.

II. Устная работа (14 мин).
1. Указать номер условия, в котором известные величины соответствуют первому признаку равенства треугольников, ∆ ABC = ∆ A1B1C1 (условия – на доске):
а) AB = A1B1, A = A1;
б) AB = A1B1, AC = A1C1, C = C1;
в) BC = B1C1, AC = A1C1, C = C1.
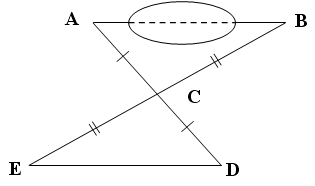
2. Чтобы измерить на местности расстояние между двумя точками А и В, между которыми нельзя пройти по прямой, выбирают такую точку С, из которой можно пройти и в точку А и к точке В и из которой видны обе эти точки. Провешивают расстояние АС и ВС, продолжая их за точку С и отмеряют СD = AC и EC = CB. Тогда отрезок ЕD равен искомому расстоянию АВ. Объясните почему (чертеж – на доске).

3. Из бумажного прямоугольника сгибанием получить равнобедренный треугольник (проверить и сформулировать свойства равнобедренного треугольника).
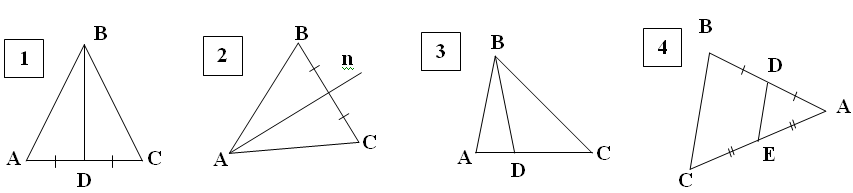
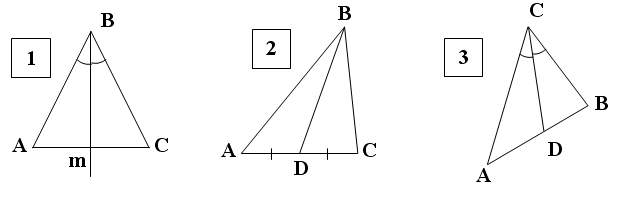
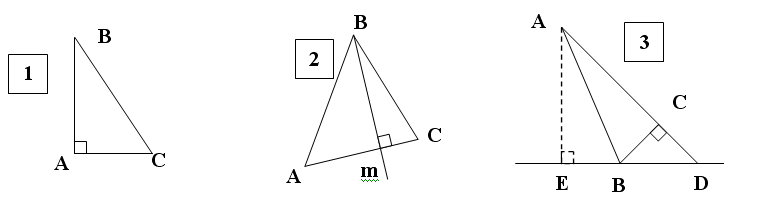
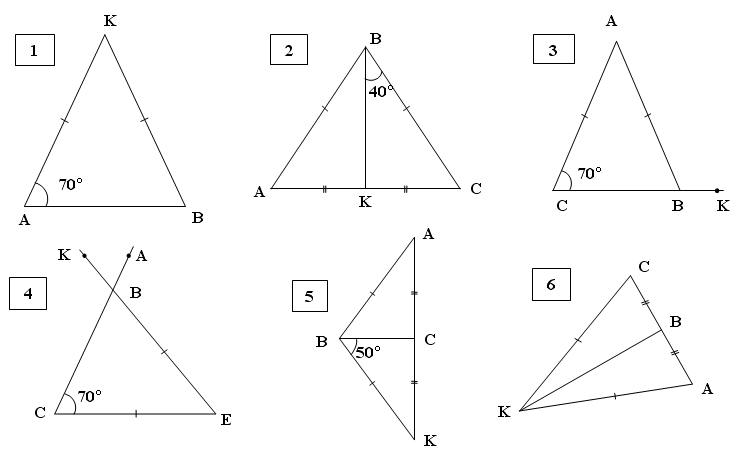
4. На каких рисунках изображены (рисунки – на графопроекторе):
а) медианы:

б) биссектрисы:

в) высоты:

5. Найти угол КВА. Чертежи на рисунках 3, 4, 6 – в тетрадь (задания – на карточке).

III. Письменное решение задач (25 мин). Задания выполняются в тетрадях, а затем у доски с полным оформлением (чертежи даны на доске, а условия читаются вслух).

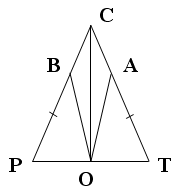
Дано: ∆ РСТ – равнобедренный, РТ – основание,
СО – высота, РВ = ТА.

Доказать: РВО = TАO.

2. Равнобедренные треугольники АВС и DВС имеют общее основание ВС. Вершины А и D находятся по разные стороны от ВС. Отрезки АD и ВС пересекаются в точке О. Докажите, что АD _|_ ВС.

3.

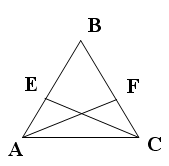
На рисунке AB = CB и AE = CF.

Доказать: AEC = CFA.

IV. Домашнее задание (3 мин):
1. Всем: На следующем уроке вам будет предложено за одну минуту начертить как можно больше равных треугольников («бенефисный» урок). Каждый из вас может подготовиться к выполнению этого задания. Подумайте и подготовьтесь.
2. Для двух учащихся (условие – на карточках): На высоте BК равнобедренного треугольника АВС (АВ=ВС), взята точка D. Доказать, что: а) ∆АВD = ∆CВD; б) ∆АDК = ∆СDK (найти четыре способа решения).
3. «Сильным» учащимся (условие – на карточках):
а) Дан равнобедренный треугольник АВС с основанием АС. Где надо отметить точку К, чтобы ∆ АКВ = ∆ СКВ?
б) Представьте себе, что равные треугольники АВС и А1В1С1 переместились так, что точки А и А1 и точки С и С1 совпали. Проведите мысленно отрезок ВВ1. Докажите, не выполняя нового чертежа, что АС ВВ1.
в) Остальным учащимся: По чертежам, выполненным на уроке, восстановить условие и записать решение в тетрадь для домашних работ.
IV. Подведение итогов урока (2 мин): выставление оценок, выявление лучшего КБ, поощрение отдельных учащихся и т. п.