Мы вывели модель, описывающую наши измерения, теперь надо определить, верна ли она. Для решения этого вопроса нужно проверить гипотезы:

Модель регрессионного анализа выглядит следующим образом:

где а–параметр, характеризующий смещение по Y, b - коэффициент регрессии – параметр, характеризующий смещение графика функции по X; ε_i – некоррелированные ошибки случайной переменной.

В регрессионном анализе проверяют гипотезы о значимости свободного члена а и о значимости коэффициента регрессии b.

Проверка гипотезы о значимости коэффициента регрессии b:
1. Определим гипотезы H₀ и H₁:
H₀: b=0 (между переменными нет линейной зависимости)
H₁: b₁≠0.
2. Зададим уровень значимости α.
3.
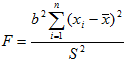
где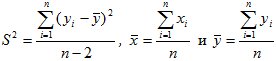
Статистика F имеет распределение Фишера с 1 и (n-1) степенями свободы.
4. Критические точки и критическая область K_кр=F_кр(α,1,n-2).
5. Если |F_набл|(α,1,n-2), то H₀ отвергается, т.е. можно сделать вывод, что линейная зависимость – значима. Если |F_набл|>F_(α,1,n-2) то у нас нет оснований отвергать H₀, т.е. можно сделать вывод, что линейная зависимость – незначима или что наши данные нельзя описать моделью линейной регрессии.