| Модератор форума: Bukashka, noka |
| Форум "Казахстан и образование"Математика геометрия Ученический форум Математика Векторы, операции с векторами. (Все задачи на векторы, решение бесплатно!) |
| Векторы, операции с векторами. |
Гость
27.12.2013, 22:39, Пятница | Сообщение 211
Вектор а = (1;2;4) найти вектор |а| помогите тему проболела
|
|
28.12.2013, 11:24, Суббота | Сообщение 212
Модуль вектора: |а|=√(1²+2²+4²)=√21 |
|
07.01.2014, 00:45, Вторник | Сообщение 213
Что получится при сложении в параллепипеде векторов СС1 и СА1? знаю ответ, но объясните пж.)
|
|
07.01.2014, 12:20, Вторник | Сообщение 214
Что получится при сложении в параллепипеде векторов СС1 и СА1? знаю ответ, но объясните пж.) 
|
|
21.01.2014, 23:38, Вторник | Сообщение 215
что-то я запуталась(( помогите: В равнобедренной трапеции ABCD вектора AB=a, AD=b, верхнее основание BC в 2 раза меньше нижнего AD. Точка К лежит на середине CD, а точка М на середине BC. Выразите через a и b сумму: ВК+АС+MD. A) 2a - 7b В) -1/2a + 2b C) 1/2 - 2b D) 1/2a + 7b E) 1/2a - 5b |
|
22.01.2014, 19:35, Среда | Сообщение 216
В равнобедренной трапеции ABCD вектора AB=a, AD=b, верхнее основание BC в 2 раза меньше нижнего AD. Точка К лежит на середине CD, а точка М на середине BC. Выразите через a и b сумму: ВК+АС+MD. Нашел на сайте уже давнишнюю запись, там только на рисунок не смотри, он ошибки содержит. А именно вектор BM равен b/4, там он в решении исправил! http://www.testent.ru/forum/6-1012-22785-16-1331289034 |
|
22.01.2014, 20:14, Среда | Сообщение 217
Составьте уравнение прямой, содержащей медиану MK треугольника MDC, если его вершины M(-2;6), D(8;-2), С(-4;-2)  Медиана MK треугольника MDC делит сторону DC пополам, найдем точку K: Вспомним как найти координаты середины отрезка. Для этого есть простая формула: x = (x₁+x₂)/2, y = (y₁+y₂)/2. K по x: (-4+8)/2 K по y: (-2-2)/2 K(2;-2) Уравнение прямой, проходящей через две точки M(-2;6) и K(2;-2): 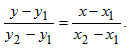
|
|
22.01.2014, 21:07, Среда | Сообщение 218
аааа... точно... надо было до параллелограмма достроить. Что-то не додумалась(
|
Гость
23.01.2014, 15:18, Четверг | Сообщение 219
помогите пожалуйста, найти вектор x, если x перпендикулярен a = (1;-1;1). x перпендикулярен оси OZ, модуль x =2 |
Надежда
05.02.2014, 01:23, Среда | Сообщение 220
Написать уравнение перпендикуляра,опущенного из точки М (-2;-1;-3) на прямую L: (x-4)/1=(y+1)/2=(z-3)/3.Заранее спасибо!!! |
|
09.02.2014, 03:04, Воскресенье | Сообщение 221
помогите пожалуйста, найти вектор x, если x перпендикулярен a = (1;-1;1). x перпендикулярен оси OZ, модуль x =2 Всего три условия, из каждого условия можно сделать уравнение а из них уже - систему. Твоя ссылка первая Написать уравнение перпендикуляра,опущенного из точки М (-2;-1;-3) на прямую L: (x-4)/1=(y+1)/2=(z-3)/3.Заранее спасибо!!! Твоя ссылка вторая |
|
24.02.2014, 11:00, Понедельник | Сообщение 222
Тема: Координаты вектора Пример 1. Даны векторы: а( 3;-2) и b(-3;4). Найти координаты вектора 2а - Зb . Найдем вектор 2a, для этого умножим x₁, y₁ на 2: (6;-4) По аналогии найдем вектор 3b: (-9; 12) Разность векторов: m-n=(mx-nx; my-ny) 2a-3b = (6+9; -4-12) = (15; -16) Пример 2. Векторы АВ(4;3) и АС(2;1) совпадают со сторонами треугольника. Определить координаты вектора медианы АК.  На рисунке показаны 2 вектора, AB и AC. Достраивая до параллелограмма, вектор AD будет равен сумме векторов AB + AC. Диагональ параллелограмма BC делит AD пополам, следовательно вектор AK равен: (AB + AC) / 2 AK = ((4+2)/2 ; (3+1)/2) = (3; 2) Пример 3. На плоскости даны два вектора a(2;4), b(8;6). Найти коэффициенты разложения вектора c(10; -10) по векторам а и b . Для решения подобных заданий, нужно составить систему уравнений: 2x+8y=10 4x+6y=-10 Решая систему уравнений, найдем корни x=-7, y=3 Тогда разложение вектора c по векторам a и b запишется как: c = -7a + 3b Пример 4. Найти координаты начала вектора а{2;-3;-1}, если концом его является точка В(1;-1;2). Для того чтобы найти вектор a, имея две точки A(x,y,z) и В(1;-1;2), от координат второй точки, нужно отнять координаты первой соответственно: 1-x=2 ⇒ x=-1 -1-y=-3 ⇒ y=2 2-z=-1 ⇒ z=3 Тогда координаты точки A(-1;2;3) Пример 5. Найти α и β, при которых векторы а{3;-1;4} и b{-4;β;a} коллинеарны. Вектора называются коллинеарным, когда лежат на параллельных прямых, следовательно никогда не пересекаются. Для решения таких заданий, достаточно составить пропорции: 3/-4 = -1/β ⇒ β=4/3 3/-4 = 4/α ⇒ α=-16/3 Пример 6. Вектор с(2m;-3) равен сумме векторов а(7m;5) и b(-18;2n), найдите m и n. 7m-18=2m ⇒ m = 18/5 5+2n=-3 ⇒ n = -4 Пример 7. Какие из перечисленных векторов являются перпендикулярным вектору a = i - j + 2k: b = 3i + j - k с = 5i - i + k d = -5i + i + 3k e = 5i + i - 2k Для того чтобы проверить, перпендикулярны ли вектора, составим нормаль вектора вектору a = (1;-1;2), b = (3;1;-1), c = (5,-1,1), d = (-5;1;3), e = (5;1;-2) Если скалярное произведение векторов равно 0, значит они перпендикулярны: 1*3 + (-1)*1 + 2*(-1) = 3-1-2=0 (вектор a перпендикулярен вектору b) 1*5 + (-1)*(-1) + 2*1 = = 5+1+2=8 (вектор a не перпендикулярен вектору c) 1*(-5) + (-1)*1 + 2*(3) = -5-1+6=0 (вектор a перпендикулярен вектору d) 1*5 + (-1)*1 + 2*(-2) = 5-1-4=0 (вектор a перпендикулярен вектору e) |
Гость
24.02.2014, 14:52, Понедельник | Сообщение 223
Найдите координаты точки S, чтобы имело место равенство NK=2*MS, где M(1;3) N(-3;1) K(3;-1).
|
Гость
24.02.2014, 15:04, Понедельник | Сообщение 224
Выразите вектор OH=(2;2) через векторы NM и NK, где M(1;3) , N(-3;1) , K(3;-1)
|
|
24.02.2014, 15:50, Понедельник | Сообщение 225
Найдите координаты точки S, чтобы имело место равенство NK=2*MS, где M(1;3) N(-3;1) K(3;-1). Пусть точка S(x,y) Вектор NK={3-(-3); -1-1}={6; -2} Вектор MS={x-1; y-3} Вектор 2MS={2x-2; 2y-6} Тогда согласно уравнению в задании: 2x-2=6 x=4 2y-6=-2 y=2 Ответ: S(4,2) |
|
24.02.2014, 15:57, Понедельник | Сообщение 226
Найдите векторы NM и NK: NM={-3-1; 1-3}={-4; -2} NK={3+3; -1-1}={6; -2} Составим систему уравнений: { -4x+6y=2 { -2x-2y=2 x=-2 y=-1 Тогда OH=-2NM-NK |
Гость
01.03.2014, 11:26, Суббота | Сообщение 227
Составьте уравнение прямой, содержащей медиану МК треугольника МДС, если его вершины М(-2:6),Д(8:-2),С(-4:-2)
|
|
01.03.2014, 11:46, Суббота | Сообщение 228
Составьте уравнение прямой, содержащей медиану МК треугольника МДС, если его вершины М(-2:6),Д(8:-2),С(-4:-2) Смотрите пример 2. Составьте векторы MD и MC. MD={8+2; -2-6}={10; -8} MC=(-4-2; -2-6)={-6; -8} Найдите сумму: MD+MC={10+(-6);-8+(-8)}={4; -16} Найдите вектор MK: MK={4/2; -16/2}={2; -8} M(-2; 6) Найдите точку K(x;y): x+2=2 ⇒ x=0 y-6=-8 ⇒ y=-2 Тогда точка K(0;-2) Составим уравнение, между точками M(-2; 6) и K(0;-2) (x-x₁)/(x₂-x₁) = (y-y₁)/(y₂-y₁) (x+2)/(0+2) = (y-6) / (-2-6) -8*(x+2) = 2*(y-6) -4*(x+2) = (y-6) -4x-8+6=y y=-4x-2 Вот так набери в гугл поиск: y=-4x-2, -0.8(x+2)+6, (8/6)*(x+2)+6 Это три уравнения, прямых MD, MC, MK |
Гость
01.03.2014, 23:53, Суббота | Сообщение 229
Добрый вечер! Помогите решить. Ромб задан вершинами А(0;3), В(3;1), С(4;-1), D(1;-1). Найти точку пересечения его диагоналей
|
|
02.03.2014, 00:12, Воскресенье | Сообщение 230
Ромб задан вершинами А(0;3), В(3;1), С(4;-1), D(1;-1). Найти точку пересечения его диагоналей Самый простой способ, это составить уравнения прямых AC и BD. Найти их пересечение: AC: x/4=(y-3)/-4 ⇒ y=3-x BD: (x-3)/-2=y-1/-2 ⇒ y=x-2 Тогда они пересекаются в точке x: 3-x=x-2 x=5/2 y=1/2 Ответ: (0.5; 2.5) Значит в вашей программе ошибка и почему то, я не удивлен!!! Проверить можно себя так: y=3-x А(0;3) С(4;-1) y=x-2 В(3;1) D(1;-1) |
Гость
02.03.2014, 01:30, Воскресенье | Сообщение 231
Я аналогичного мнения, что ошибка в программе. Помогите еще пожалуйста: Вычислить: |а|² + |c|² - (ab)(bc), если а = (-2;0;3), b = (2;-2;0), c = (2;-2;3) , где все - abc вектор.
|
|
02.03.2014, 22:15, Воскресенье | Сообщение 232
Гость, я одного не могу понять, зачем вот это было писать где все - abc вектор. Что еще за слово все ??? А решается просто: Модуль вектора |a|=√(x²+y²+z²), где x,y,z - координаты вектора a. (a,b) - скалярное произведение, найти можно: (a,b) = x₁x₂+y₁y₂+z₁z₂, где x₁, y₁, z₁ - координаты вектора a, x₁, y₁, z₁ - координаты вектора b Дальше самостоятельно, формулы у вас есть! Ответ должен быть 62! |
|
05.03.2014, 15:36, Среда | Сообщение 233
Тема: Уравнение прямой Пример 1. Написать уравнение прямой, проходящей через точки А(-1;1) и В(2;5). Воспользуемся формулой: (x-x₁)/(x₂-x₁) = (y-y₁)/(y₂-y₁) Координаты точек A (x₁; y₁), B (x₂,y₂). Составим уравнение: (x+1)/3=(y-1)/4 ⇒ 4x-3y+7=0 Пример 2. На прямой х +2у -1=0 найти точку равноудалённую от точек A(-2;5) и B(0;1). Пусть на прямой лежит точка M(x,y), тогда модуль вектора AM равен, модулю вектора MB. AM=(x+2; y-5) BM=(x; 1-y) Теперь модуль вектора AM приравняем к модулю вектора BM: (x+2)² + (y-5)² = x² + (1-y)² x²+4x+4+y²-10y+25=x²+1-2y+y² 4x-8y=-28 x-2y=-7 Теперь, раз точки x и y лежат прямой, значит можно составить систему уравнений: { x=2y-7 { х +2у -1=0 Решая найдем: y=2, x=-3 Тогда точка M имеет координаты (-3; 2) Пример 3. Уравнение прямой, проходящей через точку А (-3;10) и перпендикулярной оси OY, имеет вид: y=10 Пример 4. Уравнение прямой, проходящей через точку А(9;3) и перпендикулярной оси ОХ, имеет вид: х=9 Пример 5. Дан треугольник ABC; А(2;-6), В(4;2), С(0;-4). Уравнение прямой, содержащей среднюю линию треугольника ABC, которая параллельна стороне АС, имеет вид:  Пусть KM - средняя линия треугольника ABC. Найдем координаты точки K и M, зная что средняя линия делит сторону AB и BC пополам? Если отрезок АВ, где А(х₁; y₁) и В(х₂; y₂) делится точкой K пополам, тогда координаты точки K(x,y) найдем: х = (х₁ + х₂)/2 у = (y₁ + y₂)/2 см. также деление отрезка в заданном соотношении. K(3; -2) M(2; -1) Теперь составим уравнение, как в 1 примере: (x-3)/-1 = y+2 y=1-x Пример 6. Найдите площадь треугольника, ограниченного линиями: у=х-2; у=-х-2; у = 0 Естественно, можно воспользоваться определенным интегралом, но в данной задаче требуется найти площадь другим способом. Построим рисунок, для этого найдем пересечение прямых у=х-2 и у=-х-2 с осями абсцисс и ординат: A(0;-2), B(-2;0), C(2;0), O(0;0)  Тогда площадь треугольника равна AO*BC/2 = 2*4/2=4 Пример 7. Расстояние от точки пересечения прямых 4х+3у-6=0 и 2х+у- 4=0 до оси ОХ равно: Найдем пересечение прямых, для этого решим систему уравнений: 4х+3у-6=0 2х+у- 4=0 |*2 {4х+3у-6=0 {4х+2у-8=0 y=-2 Тогда точка пересечения имеет координаты (x, -2), а значит удалена от OX на 2 единицы. Пример 8. Расстояние от точки пересечения прямых 4х+3у-6=0 и 2х+у-4=0 до начала координат равно. Уравнения те же, значит y=-2, x=3 Тогда расстояние от точки пересечения до OY равно 3, до OX равно 2, а до начала координат по теореме Пифагора, гипотенуза равна √13 Пример 9.  Определите площадь закрашенной фигуры, если прямая l параллельная прямой m. Составим уравнение прямой l и запишем в общем виде y=kx+b, , где b∈(-∞;+∞): x/12=(y+9)/9 y=(9/12)*x-9=(3/4)*x-9 Теперь составим уравнение для прямой m: x/n=y/12 y=(12/n)*x У параллельных прямых коэффициент k будет равен. Следовательно можно записать: 12/n=3/4 Отсюда n=16 Тогда площадь фигуры равна 16*12=192 Пример 10. Уравнение прямой, проходящей через точку М(7;-11) и параллельно прямой у = -2х+5, имеет вид: Прямая задана уравнением с угловым коэффициентом k=-2, параллельные прямые имеют равный коэффициент k, поэтому уравнение прямой проходящей через точку S(x₀,y₀), для прямой вида y=kx+b можно найти по формуле: y-y₀=k(x-x₀) Тогда прямая, проходящая через точку M примет вид: y-(-11)=-2(x-7) ⇒ y+11=-2x+14 ⇒ y=-2x+3 Пример 11. Если прямая проходит через точки А(2;3) и В(3;2), то сумма коэффициентов а и b в уравнении ах+by=1 равна: Составим уравнение прямой AB: (x-2)/1=(y-3)/-1 x-2=-y+3 x+y=5 Приведем его к виду ах+by=1 (x/5) + (y/5) = 1 Тогда сумма коэффициентов a+b равна 2/5 Пример 12. Найти угловой коэффициент прямой, проходящей через точки А(1;-1) и В( 2;3). Составить уравнение прямой и записать его в виде y=kx+b 4x-4=y+1 ⇒y=4x-5 k=4 Пример 13. При каком k точки А(2;1), В( 3;-2), С(0; k) лежат на одной прямой: Составить уравнение прямой между точками A и B, подставить значение x точки C и найти k: x-2=(y-1)/-2 -3x+6=y-1 y=-3x+7 При x=0, y=7 |
Гость
13.03.2014, 21:09, Четверг | Сообщение 234
Даны векторы: a (3;-2;-8) b (4; 0;-2) найти вектор а+b; a-b Помогите |
|
13.03.2014, 23:43, Четверг | Сообщение 235
a(x1;y1;z1) b (x2;y2;z2) Сложение векторов : a+b=(x1+x2;y1+y2;z1+z2) Разность векторов : a-b=(x1-x2;y1-y2;z1-z2) |
Гость
20.03.2014, 23:32, Четверг | Сообщение 236
Артем, обьясните как решать задачу. Найти все точки М(х,у) для которых |МА|=2 угол МАВ =60 А(1,1) В(3,1) |
|
06.04.2014, 12:15, Воскресенье | Сообщение 237
Найдите острый угол A ромба с вершинами А(-2;-2), В(4,2), С(10;-2), D(4;-6) Обозначим точку пересечения диагоналей O(4;-2), тогда BO=4, AO=6 По теореме Пифагора: AB = √52 Теперь по теореме косинусов для треугольника ABD: BD²=AB²+AD²-2*AB*AD*cosα 8^2=52+52-2*52*cosα 64=104(1-cosα) 1-cosα=64/104 cosα=1-(64/104)=40/104=20/52=10/26=5/13 α=arccos(5/13) |
Гость 2
07.04.2014, 17:40, Понедельник | Сообщение 238
Помогите пожалуйста решить. В параллелограме ABCD: векторы AB(2;-10;1), AD(5;8;-2), и точка A(1;2;-1). Тогда сумма координат точки C равна ____.
|
|
17.04.2014, 23:01, Четверг | Сообщение 239
Здравствуйте! Пожалуйста, помогите с решением: Даны точки Р(2,-2) Q(4,0) R(0,4) 1) РT- медиана треугольника PQR. Найдите координаты вектора PT 2) Найдите |2PQ+QR| 3) Найдите угол PQR |
|
17.04.2014, 23:06, Четверг | Сообщение 240
В треугольнике КМН угол К 45 градусов, КМ=МН, КН=8 см. Медиана МR и КР пересекаются в точке О 1) Выразите векторы ОМ и ОР через вектор а=вектору КR и вектор в=вектору КМ 2) Найдите |ОR| и |МР| |
| |||
 Друзья сайта
Друзья сайта Ученики
Ученики