ОБОРУДОВАНИЕ: установка, состоящая из стеклянного баллона, манометра, компрессора, секундомер.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Теплоемкостью вещества называется физическая величина, численно равная количеству теплоты, которое нужно ему сообщить, чтобы повысить температуру вещества на один кельвин.
Теплоемкость единицы массы называется удельной теплоемкостью, а теплоемкость одного моля вещества - молярной теплоемкостью.
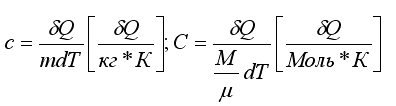
где с и С - удельная и молярная теплоемкость,
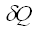- теплота, подводимая к системе,
dT - изменение температуры,
m - полная масса вещества,
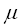- его молекулярная масса.
Величина теплоемкости для одного и того же вещества зависит как от агрегатного состояния, так и от условий его нагревания.
Нагревание вещества может происходить как при постоянном давлении, так и при постоянном объеме. Рассмотрим эти процессы.
а) P = const . Процесс изобарический.
Первое начало термодинамики для изобарического процесса имеет вид:
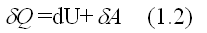
изменение внутренней энергии идеального газа:
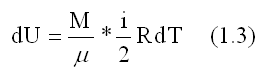
Элементарная работа при равновесном изменении объема, вычисленная из уравнения состояния газа:
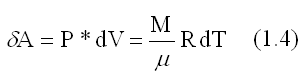
Из выражений (1.1), (1.2), (1.3), (1.4) получаем для молярной теплоемкости при постоянном давлении:
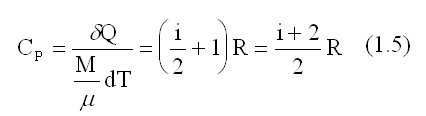
где: i - число степеней свободы молекул газа - это число независимых координат, определяющих положение молекулы в пространстве: i =3 для одноатомной, i=5 для двухатомной, i=6 для трёх- и многоатомной;
R = 8,31 Дж/моль. R - универсальная газовая постоянная.
б) V = const . Процесс изохорический.
Первое начало термодинамики для изохорического процесса
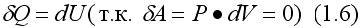
т.е. вся подводимая теплота идет только на изменение внутренней энергии системы. С учетом выражения (1.1) и (1.3) имеем
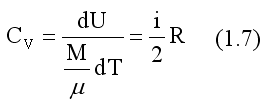
таким образом, теплоемкость идеального газа зависит только от рода газа ( i ) и от вида процесса.
в) В технике при анализе тепловых процессов и циклов как правило нет необходимости вычислять или экспериментально определять по отдельности теплоемкости при постоянном давлении Ср и при постоянном объеме Сv. Вычисление и измерение их связано с определенными трудностями (многокомпонентный газ, ничтожная масса газа по сравнению с сосудом, его содержащим и т.д.).
Во многих случаях достаточно знания только их отношения:
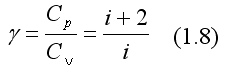
где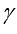 
- называют показателем адиабаты или коэффициентом Пуассона.
Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой.
Из 1 начала термодинамики для адиабатического процесса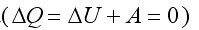 
следует:
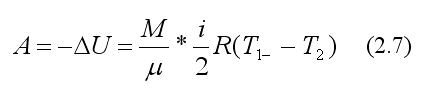
т.е. газ расширяясь совершает работу против внешних сил за счет уменьшения своей внутренней энергии.
В выражении (2.7) работа выражена через изменение температуры, а так как в эксперименте измеряется давление, то произведем изменение параметров.
Из уравнения состояния имеем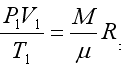 
подставим в уравнение (2.7)
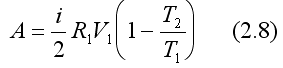
Учитывая, что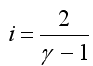 
и из выражения (2.3) следует:
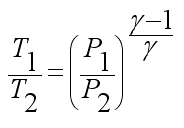
Окончательно получаем:
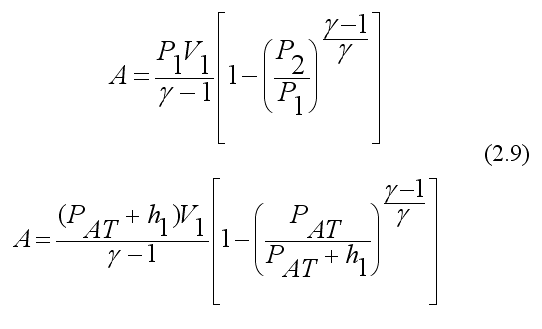
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
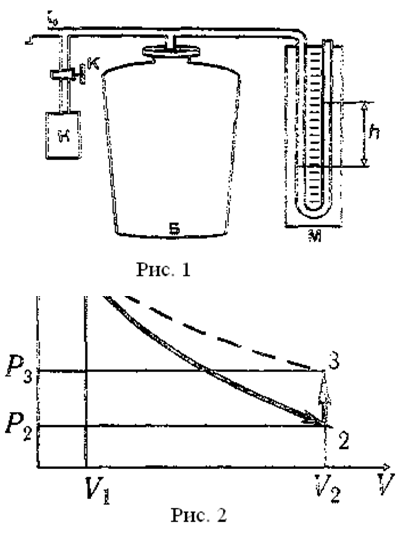Измерения выполняют на установке (рис. 1), состоящей из большого стеклянного баллона Б, насоса Н и водяного манометра 1. Баллон соединяют краном К с насосом, а краном K0 - с атмосферой.
Метод, предложенный Клепаном и Дезормом (1819 г.), основан на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами: адиабатическим и изохорическим.
Эти процессы на диаграмме P—V (рис.1) представлены кривыми 1-2 и 2-3 соответственно. Если накачать воздух в баллон и выдержать до установления теплового равновесия с окружающей средой, то в этом начальном состоянии 1 газ имеет параметры Р1, V1, T1 причём температура газа в баллоне равна температуре окружающей среды, а давление Р1=Р0+P' немного больше атмосферного Р0.
При открывании крана К0 воздух в баллоне перейдёт в состояние 2. Его давление снизится до атмосферного Р2=Р0. Оставшаяся масса воздуха, которая занимала в состоянии 1 часть объёма баллона, расширяясь, займёт весь объем V2. При этом температура воздуха, оставшегося в баллоне, уменьшится. При быстром расширении газа можно пренебречь его теплообменом с окружающей средой через стенки баллона и считать процесс 1-2 адиабатическим:
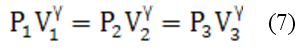
После закрытия крана Ко охлаждённый адиабатическим расширением воздух в баллоне будет нагреваться (процесс 2-3) до температуры окружающей среды T3=T1 при постоянном объёме V2= V3 При этом давление в баллоне возрастёт до Р3=Р2+Р”
Избыточное давление воздуха P’ и P’’ измеряют с помощью U-образного манометра по разности уровней жидкости с плотностью р:
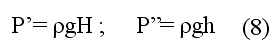
где H и h — показания манометра в состояниях 1 и 3 соответственно.
Тогда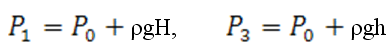 
Состояния воздуха 1 и 3 принадлежат – изотерме, поэтому:
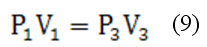
Исключив отношение объёмов из уравнений (7) и (9), найдём связь давлений газа:
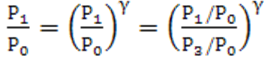
Выразим давления P1 и P2 через P0 с учётом (8.8) к прологарифмируем:
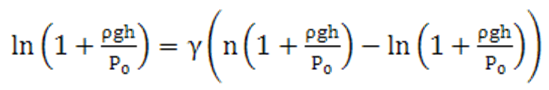
С учётом того, что если x<<1. тс ln(1+х)= x, получим расчётную формулу в следующем виде:
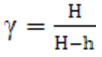
Таким образом, для определения отношения теплоёмкостей воздуха достаточно осуществить процессы (1-2-3) и измерить показания манометра Н и h в состояниях газа 1 и 3 соответственно. Логарифмируя эту функцию, получаем зависимость где а - постоянная установки, Построив по данным эксперимента такой график, можно путём экстраполяции опытной прямой до t=0 - определить значение In h, а по нему значение h, необходимое для расчёта Контрольные вопросы
Но осуществить равновесный адиабатический процесс сложно: если проводить расширение газа быстро, то процесс не будет равновесным, так как температура и давление газа не успевают выравниваться по объёму. Для проведения медленного адиабатического процесса нужна тепловая изоляция баллона. 3 данной установке за время / расширения газа подводится тепло. Поэтому при последующем изохорическом нагревании давление поднимается меньше, т.е. измеряемое h’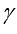 По мере увеличения времени расширения газа значение h’ снижается, приближаясь к нулю при t → ∞ (изотермическое расширение 1-3), Опытным путем установлено, что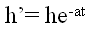 
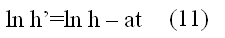
t - время протекания процесса, в течение которого баллон сообщается с атмосферой. График зависимости (11) конечного избыточного давления воздуха в баллоне от времени контакта его с атмосферой показан на рис. 3.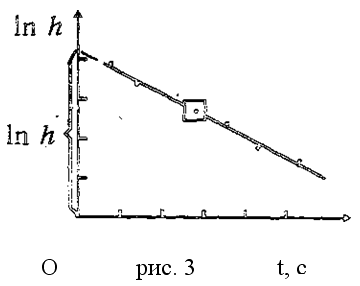 
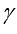по формуле (10).
1. Что называют: а) теплоёмкостью тела; б) удельной теплоёмкостью газа; в) молярной теплоёмкостью газа? В каких единицах их измеряют?
2. От чего зависят эти теплоёмкости?
3. Каковы величины молярных теплоёмкостей Ср и Сv для воздуха? Чем объясняется, что Ср> Сv?
4. Для каких теплоёмкостей справедливы соотношения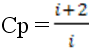 
Cp = C v+ R ?
5. Что называют числом степеней свободы молекулы?
6. Каковы значения показателя адиабаты 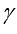а) для двухатомного; б) для трехатомного и многоатомного идеального газа?
7. Для какого газа: одноатомного ели двухатомного - график адиабаты более крутой?
8. Запишите первое начало термодинамики для адиабатического процесса.
9. Какие процессы описываются уравнениями: PV = const;
10. Как изменяется температура и давление газа: а) при адиабатическом
расширении; б) при адиабатическом сжатии?
11. В каких состояниях из указанных на диаграмме (рис. 2, с. 89) воздух в баллоне: а) имеет комнатную температуру; б) находится при атмосферном давлении?
12. Какой процесс совершается при открывании крана K2, если в баллоне было избыточное давление воздуха?
13. Какой процесс происходит после адиабатического расширения газа при проведении опыта?
14. Какие величины измеряют в работе для расчёта показателя адиабаты ?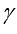
15. По какой формуле определяют значение отношения теплоемкостей 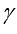а) опытное; б) теоретическое?
