ОБОРУДОВАНИЕ: специальная установка, секундомер, линейка.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Колебаниями называют процессы, в той или иной степени повторяющиеся по времени.
Свободными, или собственными, называют такие колебания, которые про¬исходят в системе, предоставленной самой себе.
Вынужденными называют колебания, происходящие под действием внеш¬ней периодически изменяющейся силы.
Гармоническими называют колебания, в которых величина х изменяется по закону:
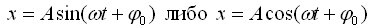
где А - амплитуда - наибольшее отклонение системы от положения равновесия, ω - циклическая частота колебаний - число колебаний за 2π секунд,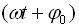 
- фаза колебаний, 
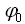- начальная фаза.
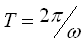- период колебаний - время одного полного колебания, за которое фаза получает приращение 2
.
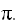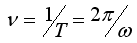частота колебаний - число колебаний за одну секунду.
Гармонические колебания происходят в системе, в которой действуют только квазиупругие силы. Квазиупругая сила - сила, независимо от своей природы изменяющаяся по закону:
где k- коэффициент упругости (жёсткость системы) или другой коэффициент пропорциональности между силой и смещением х; х - смещение колеблющейся системы от положения равновесия.
ОПИСАНИЕ УСТАНОВКИ
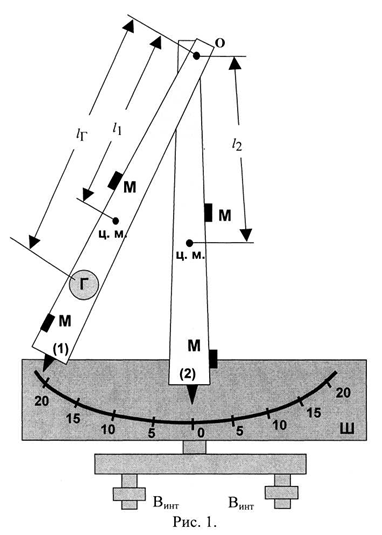
Установка состоит из двух физических маятников (1) (масса m1) и (2) (масса m2), которые независимо могут вращаться вокруг общей оси О (рис. 1). Маятники снабжены магнитами М, с помощью которых они стягиваются и могут вра¬щаться вокруг оси О как единое целое. Для изменения момента инерции к маятнику 1 может быть при¬креплен добавочный груз Г (масса mГ).
На каждом маятнике красной меткой указано положение центра масс (ц.м.), расстояние которого от оси вращения равны, соответственно,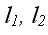 
Очевидно, центр масс маятника с добавочным грузом находится от оси вращения на расстоянии:
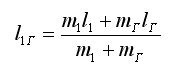
где lГ - расстояние центра груза от оси вращения.
Центр масс двух маятников с добавочным грузом находится от оси вращения на расстоянии:
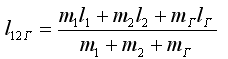
Если добавочный груз отсутствует, то это расстояние:
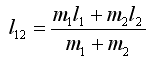
Угол отклонения маятника от положения равновесия определяется по шкале Ш. В положении равновесия маятники располагаются так, чтобы их визиры находились против нулевой отметки шкалы Ш. Это достигается с помощью винтов В в основании установки.
Если отклонить один из маятников, и закрепить в отклоненном положении, а второй отклонить и отпустить, то он будет совершать колебательное движение около положения равновесия.
Если же один из маятников отклонить из положения равновесия на угол α (второй при этом оставить в положении равновесия) и отпустить, то после столкновения маятников они начнут двигаться как одно целое и отклонятся от положения равновесия на угол β.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
Два физических маятника, имеющие общую горизонтальную ось вращения образуют замкнутую систему в момент прохождения ими положения равновесия (в этом положении моменты сил тяжести равны нулю, а других моментов относительно оси вращения просто нет). Следовательно, при прохождении положения равновесия для этой системы выполняется закон сохранения момента импульса:
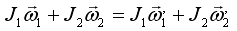
где J1 и J2- моменты инерции маятников относительно оси вращения; и - их угловые скорости в положении равновесия до их соударения;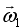 
и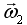 
- их угловые скорости после взаимодействия.
До взаимодействия второй маятник покоится 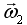= 0, а после взаимодействия оба маятника движутся как единое целое ==
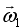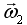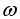и поэтому закон сохранения момента импульса в проекции на ось вращения принимает вид:
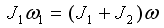
Моменты инерции маятников можно найти, зная их периоды колебаний:
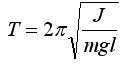
где l - расстояние от оси вращения до центра масс маятника.
Таким образом, момент инерции маятника 1
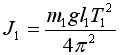(без добавочного груза);
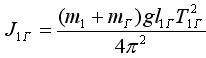(с грузом)
момент инерции системы из двух маятников
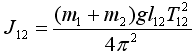(без добавочного груза);
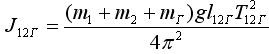(с грузом)
где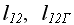 
- расстояние от оси до центра масс системы из двух маятников без дополнительного груза и с грузом;
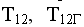- период колебания системы из двух маятников (без груза и с грузом).
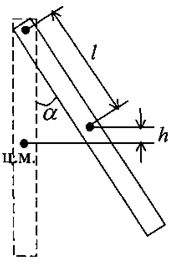
При отклонении маятника от положения равновесия на угол α центр масс его поднимется на высоту (рис. 2)
h = l (1 – cos α).
Так как до взаимодействия и после взаимодей¬ствия на маятник действует только сила тяжести (консервативная), а момент силы сопротивления достаточно мал, из закона сохранения механической энергии:
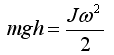
можно найти угловую скорость маятника в момент прохождения положения равновесия:
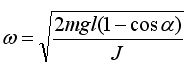
где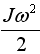 
энергия колеблющегося маятника при прохождении положения равновесия, mgh - энергия маятника, отклоненного на угол α (при этом его центр масс поднят на высоту h).
В наших опытах первоначально маятник 1 отклоняется от положения равновесия на угол α и, следовательно, его угловая скорость при прохождении положения равновесия (т.е. перед взаимодействием (столкновением) с маятником В)):
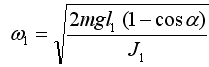(без добавочного груза);
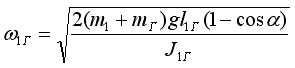(с грузом)
После столкновения система из двух маятников отклоняется на угол β и следовательно, их начальная угловая скорость в положении равновесия :
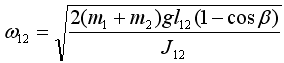(без добавочного груза);
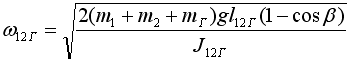(с грузом)
ВОПРОСЫ К ДОПУСКУ
1. Что такое математический маятник? физический маятник?
2. От чего зависит период малых колебаний физического маятника?
3. Что называется моментом импульса материальной точки, тела? Как направлен момент импульса?
4. Запишите закон сохранения момента импульса системы из двух маятников.
5. Как можно определить начальную скорость маятника до взаимодействия? Какие величины измеряют для этого?
6. От каких величин зависит момент инерции маятника? Как его изменяют в данной установке?
7. Что такое центр масс?
8. Как рассчитывают расстояние до центра масс системы из двух маятников?
9. От чего зависит угловая скорость маятника перед взаимодействием?
10. Чему равна энергия маятника: перед взаимодействием? после взаимодействия?
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чём состоит метод определения ускорения свободного падения с по¬мощью математического маятника? Физического маятника?
2. В чём могут состоять причины различия ускорения свободного падения, определённого экспериментально, и известного значения (g=9,8l м/с2)?
3. Почему угловая амплитуда колебаний маятника не должна превышать пяти градусов?
4. Как можно изменить период колебаний физического маятника? Приве¬дённую длину?
5. Как будет вести себя физический маятник, если совместить точку его подвеса с центром масс?
6. Как зависит величина ускорения свободного падения от широты?
7. Что произойдёт с периодом колебаний при переносе математического маятника с полюса на экватор?
8. Будут ли работать маятниковые часы на искусственном спутнике зем¬ли? Ответ обосновать.
9. Как следует изменить длину маятника при отставании часов?
10. Определить высоту, на которой ускорение свободного падения со¬ставляет 25% от ускорения свободного падения у поверхности Земли?
11. Как с помощью какого- либо маятника можно оценить массу планеты?