ОБОРУДОВАНИЕ: специальная установка, набор гирь, штангенциркуль, секундомер
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Работа, которую совершает постоянный момент силы М при повороте тела на угол φ (в радианах),
А = Мφ (1)
Работа сил трения или сопротивления равна изменению механической энергии системы: А = Е1 – Е2 (2) Кинетическая энергия тела массой m, которое движется поступательно со скоростью υ и одновременно вращается с угловой скоростью ω относительно центра масс,
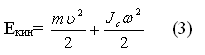
Эта энергия равна кинетической энергии вращательного движения относительно мгновенной оси (MOB):
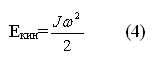
В этих формулах Jс - момент инерции тела относительно оси, проходящей через центр масс, J - момент инерции относительно MOB.
Если эти оси параллельны друг другу, то согласно теореме Штейнера
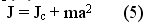
где m - масса тел, а - расстояние между осями.
ОПИСАНИЕ УСТАНОВКИ
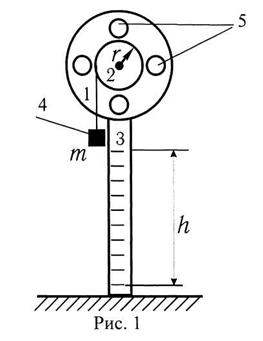
Диск 1 с резьбовыми отверстиями насажен на ось (рис. 1) и может вращаться с малым трением. На той же оси находится шкив 2 радиусом г, на который наматывается нить. К другому концу нити привязан груз 4 массой m, под действием которого система приводится во вращение.
Путь, пройденный грузом до своего нижнего положения (когда нить полностью размотается), определяется по шкале 3, вдоль которой груз движется.
В резьбовые отверстия диска могут вворачиваться дополнительные грузы 5 цилиндрической формы (радиуса R) и массы m0.
В установке предусмотрено автоматическое измерение времени движения груза до нижней точки и расстояния h, на которое поднимается груз по инерции после прохождения нижнего положения.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
Если намотать нить на шкив, подняв на высоту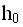 
груз m, то он будет обладать потенциальной энергией 
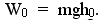При падении груза его потенциальная энергия переходит в кинетическую энергию поступательного движения груза 
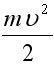и энергию вращения диска 
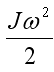. Зная время t падения груза до нижней точки, можно определить конечную скорость движения груза 
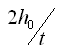и угловую скорость вращения диска 
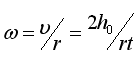, где r - радиус шкива.
При движении в подшипниках действует момент сил трения Мтр, для преодоления которого на пути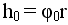 
совершается работа А = Мφ
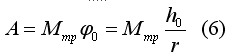
Где φ0- угол поворота диска (угловое перемещение).
В соответствии с законом сохранения энергии и равенством (2)
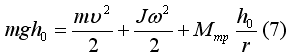
Момент сил трения Мтр найдём из следующих соображений. После того, как груз опустится до нижней точки, маховик, продолжая вращение по инерции, поднимет груз на высоту h; там его потенциальная энергия mgh меньше, чем начальная, на величину работы, совершенной против сил трения на всём пути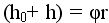 
. Из закона сохранения энергии и формулы (2) следует
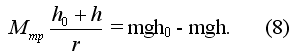
Решая совместно уравнения (7), (8), получаем расчётную формулу для момента инерции вращающегося тела:
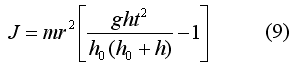
ВОПРОСЫ К ДОПУСКУ
1. Чему равен момент инерции материальной точки?
2. От каких величин зависит момент инерции диска?
3. Чему равен момент инерции твёрдого тела относительно оси?
4. В каких единицах измеряют момент инерции?
5. Чему равен момент инерции системы тел относительно какой-то оси?
6. Запишите закон сохранения энергии для системы "диск—груз".
7. На что расходуется механическая энергия в системе:
а) потенциальная энергия груза при его опускании;
б) кинетическая энергия системы при движении груза вверх?
8. Какое положение груза соответствует наибольшей кинетической энергии маховика?
9. По какой формуле определяют работу, затраченную на преодоление сил трения?
10. Чему равна работа постоянного момента силы?
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем состоит метод определения момента инерции диска в данной работе? По какой формуле его рассчитывают в опытах?
2. Чем обусловлена погрешность в данной работе?
3. От каких величин зависит кинетическая энергия тела при поступательном и вращательном движениях?
4. Что характеризует момент инерции материальной точки, тела?
5. От каких величин зависит момент инерции тела?
6. Сформулируйте и докажите теорему Штейнера.
7. Как рассчитывают момент инерции твёрдого тела сложной формы?
8. Найти момент инерции однородной пирамиды, основанием которой служит квадрат со стороной a, относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.
9. Две материальные точки с массами m1 и m2 соединены жестким невесомым стержнем длины l. Найти момент инерции этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.
