Двумерной случайной величиной называется система из двух одномерных случайных величин X, Y, где как X, так и Y являются дискретными случайными величинами.
Определим событие A: В результате испытания над двумерной случайной величиной XY, случайная величина X приняла значение xi, случайная величина Y - любое значение. То есть:
A:{xiyi,...,xiym}, тогда P(A)=P(X=xi)=P(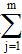 (xiyj))=
(xiyj))=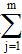 P(xiyj)=P(xi)
P(xiyj)=P(xi)
Введем событие B: В результате испытания над двумерной случайной величиной XY, случайная величина Y приняла значение yi. То есть:
B:{xiyj,...,xsyj}, тогда P(B)=P(Y=yj)=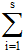 P(iyj)=P(yj)
P(iyj)=P(yj)
Найдем условную вероятность:
P(B/A)=P(y=yj/x=xi)=P(yj/xi)=P(AB)/P(A)=P(xiyji)=P(xiyj)
Аналогично:
P(A/B)=P(x=xi/y=yj)=P(xi/yj)=P(AB)/P(B)=P(xiyj)=P(xiyj)
Покажем что сумма условных вероятностей: 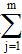 P(yj/xi)=1;
P(yj/xi)=1; 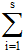 P(xi/yj)=1
P(xi/yj)=1
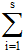 [P(xiyj)/P(yj)]=
[P(xiyj)/P(yj)]=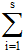 P(xiyj)/P(yj)=P(yj)/P(yj)=1
P(xiyj)/P(yj)=P(yj)/P(yj)=1
Условным математическим ожиданием является выражение:
M(y/x=xi)=y(xi)=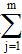 yjP(yj/xi); M(x/y=yj)=x(yj)=
yjP(yj/xi); M(x/y=yj)=x(yj)=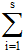 xiP(xi/yj)
xiP(xi/yj)
Условной дисперсией называется выражение:
D(y/x=xi)=σ2y/xi=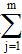 (yj-y(xi))2•P(yj/xi); D(x/y=yj)=σ2x/yj=
(yj-y(xi))2•P(yj/xi); D(x/y=yj)=σ2x/yj=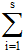 (xi-x(yj))2•P(xi/yj)
(xi-x(yj))2•P(xi/yj)
Условное мат. ожидание и дисперсия отличаются от безусловной только тем, что в их определении подставляется условная вероятность вместо безусловной. Условное мат. ожидание случайной величины, при условии, что другая случайная величина приняла заданное значение определяет число-точку, относительно которой группируются результаты конкретных испытаний над одной случайной величиной, при условии, что в этом испытании (над двумерной случайной величиной XY) вторая случайная величина приняла заданное фиксированное значение. Условная дисперсия определяет степень концентрации результатов конкретных испытаний над одной случайной величиной относительно условного мат. ожидания.
