Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них красные, 3-синие и 1-белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появление цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
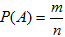 (1)
(1)где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Пример 1 Найти вероятность события А={появление не менее пяти очков при одном бросании игральной кости}.
Используем формулу (1). В нашем случае число возможных исходов n=6, а число, благоприятствующих этому событию исходов, m=2. То есть P(A)=2/6=1/3. Итак, вероятность появления не менее пяти очков при одном бросании игральной кости равна 0.33 или 1/3
Из определения вероятности вытекают следующие ее свойства:
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1
Свойство 2. Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0
Итак, вероятность любого события удовлетворяет двойному неравенству
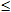 P(A)
P(A)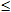 1
1