В декартовых прямоугольных координатах уравнение любой плоскости приводиться к виду

Ax+By+Cz+D=0 (14)

Уравнение (14) называется общим уравнением плоскости. Коэффициенты A,B,C являются координатами вектора 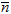, перпендикулярного к плоскости, заданной уравнением (14). Он называется нормальным вектором этой плоскости и определяет ориентацию плоскости в пространстве относительно системы координат.

Существуют различные способы задания плоскости и соответствующие им виды уравнения.

1. Уравнение плоскости по точке и нормальному вектору. Если плоскость проходит через точку M₀(x₀,y₀,z₀) и перпендикулярна к вектору 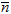=(A,B,C), то ее уравнение записывается в виде: A(x-x₀)+B(y-y₀)+C(z-z₀)=0

2. Уравнение плоскости в «отрезках». Если плоскость пересекает оси координат O_x, O_y, O_z в точках M₁(a,0,0) M₂(0,b,0) M₃(0,0,c) соответственно, то ее уравнение можно записать в виде:
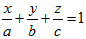(16)
где a≠0, b≠0, c≠0

3. Уравнение плоскости по трем точкам. Если плоскость проходит через точки M_i(x_i,y_i,z_i (i=1,3), не лежащие на одной прямой, то ее уравнение можно записать в виде:

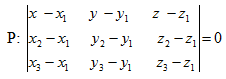(17)

Рассмотрим простейшие задачи.

1) Величина угла φ между плоскостями A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0 вычисляется на основании формулы:

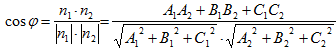(18)

где n₁=(A₁,B₁,C₁), n₂=A₂,B₂,C₂)- нормальные векторы данных плоскостей. С помощью формулы (5) можно получить условие перпендикулярности данных плоскостей:
n₁•n₂=0 или A₁A₂+B₁B₂+C₁C₂=0
Условие параллельности рассматриваемых плоскостей имеет вид:

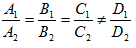
2) Расстояние d от точки до плоскости, заданной уравнением (14), вычисляется по формуле:

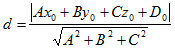
Пример 14. Вычислить расстояние между параллельными плоскостями
3x+3y+2z–15=0 и 3x+3y+2z+13=0.

Для решении задачи находим любую точку принадлежащую на одной из плоскости, например считая y=z=0 из уравнения первой плоскости находим , что x=5 Тогда по формуле нахождения расстояния от данной точки М₀(5,0,0) до второй плоскости находим d= 4.