Материалы по теме: угловой коэффициент, угол между прямыми, уравнение прямой, лекция по высшей математики, высшая математика

Пусть прямые l1 и l2 заданы уравнениями: l1: y=k1x+в1 l2: y=k2x+в2 c углами наклона к оси Ох соответственно φ1 и φ2 (рис.2). Обозначим через φ1 угол наклона прямой l1 к оси Ох и через φ угол, на который нужно повернуть прямую l1 до совпадения с l2 (рис. 6). Тогда φ1+φ=φ2 будет, очевидно, углом наклона прямой l2 к оси Oх. Отсюда φ=φ2-φ1 и если прямые l1 и l2 не являются перпендикулярными, то (по известной формуле тригонометрии) Заметив, что tgφ1=k1 и tgφ2=k2 получим: 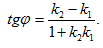(9) Пример 5. Найти угол между прямыми y=2x-3 и 3x+y-2=0 Решение: Если перенумеровать прямые в том порядке, как они заданы, то угловой коэффициент прямой l1 будет k1=2 а для прямой l2 будет k2=-3 Тогда по формуле (9) получим 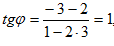откуда φ=450

1 2 3 4 5   26.07.2010     6396     3.0/2     0     Артем   Теги: угловой коэффициент, угол между прямыми, уравнение прямой, лекция по высшей математики, высшая математика

Похожие статьи: Уравнение прямой линии с угловым коэффициентом Уравнение прямой, проходящей через данную точку в данном направлении Уравнение прямой, проходящей через две данные точки Условия параллельности и перпендикулярности двух прямых Общее уравнение прямой Взаимное расположение двух прямых на плоскости Расстояние от точки до прямой

Имя *:

Код *: