(где А, В и С- постоянные коэффициенты, причем А2+В2≠0) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Частные случаи:
1. С=0; А≠0; В≠0. Прямая, определяемая уравнением Ах+Ву=0, проходит через начало координат.
2. А=0, В≠0; С≠0. Прямая, определяемая уравнением Ву+С=0 (или у=b, где 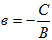 ), параллельна оси (ох).
), параллельна оси (ох).
3. В=0; А≠0; С≠0. Прямая, определяемая уравнением Ах+С=0 (или 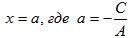 ), параллельна оси Оу.
), параллельна оси Оу.
4. В=С=0; А≠0. Прямая определяемая уравнением Ах=0 (или x=0 поскольку А≠0), совпадает с осью Оу.
5. А=С=0; В≠0. Прямая, определяемая уравнением Ву=0 (или у=0, поскольку В≠0), совпадает с осью Oх.
Если в общем уравнении прямой В≠0, то, разрешив его относительно у, получим уравнение вида y=kx+в (здесь 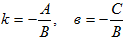 ). Его называют уравнением с угловым коэффициентом поскольку где -угол, образованный прямой с положительным направлением оси Oх. Свободный член уравнения в равен ординате точки пересечения прямой с осью Oу.
). Его называют уравнением с угловым коэффициентом поскольку где -угол, образованный прямой с положительным направлением оси Oх. Свободный член уравнения в равен ординате точки пересечения прямой с осью Oу.
|
|
 |
Fredy 03.08.2012 07:57 Gosh, I wish I would have had that information earleir!
|