Изменение энтропии
В замкнутой системе для обратимых процессов ΔS=0; для необратимых циклов ΔS>0.
Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов):
Поскольку dS и δQ имеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела δQ>0 и его энтропия возрастает dS>0, при охлаждении δQ<0 и энтропия тела убывает dS<0.
Изоэнтропийным называется процесс, протекающий при постоянной энтропии (S=const).
В обратимом адиабатическом процессе δQ=TdS=0, так что dS=0 и S=const, поэтому адиабатический процесс является изоэнтропийным.
Рассмотрим для примера идеальный газ, совершающий равновесный переход из состояния 1 в состояние 2. Изменение его энтропии:
Используя dU=(m/M)·CVdT; δA=pdV=(m/M)·RT·(dV/V); R=Cp-CV и T2V1/T1V2=p2/p1:
и окончательно,
Неравенство Клаузиуса: энтропия замкнутой системы может либо возрастать (в случае необратимых процессов) либо оставаться постоянной (в случае обратимых процессов):
ΔS≥0. (67)
Поскольку dS и δQ имеют один и тот же знак, то по характеру изменения энтропии можно судить о направлении процесса теплообмена. При нагревании тела δQ>0 и его энтропия возрастает dS>0, при охлаждении δQ<0 и энтропия тела убывает dS<0.
Изоэнтропийным называется процесс, протекающий при постоянной энтропии (S=const).
В обратимом адиабатическом процессе δQ=TdS=0, так что dS=0 и S=const, поэтому адиабатический процесс является изоэнтропийным.
Рассмотрим для примера идеальный газ, совершающий равновесный переход из состояния 1 в состояние 2. Изменение его энтропии:
ΔS1→2=S2-S1=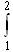
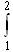δQ/T=(dU+δA)/T.
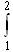δQ/T=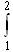(dU+δA)/T.Используя dU=(m/M)·CVdT; δA=pdV=(m/M)·RT·(dV/V); R=Cp-CV и T2V1/T1V2=p2/p1:
ΔS1→2=(m/M)·CV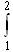(dT/T)+(m/M)·R
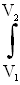dV/V=(m/M)·[CVln(T2/T1)+R·ln(V2/V1)],
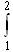(dT/T)+(m/M)·RdV/V=(m/M)·[CVln(T2/T1)+R·ln(V2/V1)],и окончательно,
ΔS1→2=(m/M)·[CV·ln(p2/p1)+Cp·ln(V2/V1)]