Для получения зависимости скорости течения жидкости по поперечному сечению трубы, воспользуемся условием стационарности. Жидкость движется с постоянной скоростью, следовательно, без ускорения, следовательно, сумма сил, приложенных к выделенному объему равна нулю. На выделенный объем действуют силы давления и силы трения:
Из условия стационарности следует:
Преобразуем полученное уравнение:
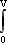 dv=[(P1-P2)/2η·L] ·
dv=[(P1-P2)/2η·L] · 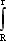 r · dr
r · drт.к. при r=R → v=0. Окончательно получим:
V=(P1-P2) · (R2-r2) / 4η·L
Это парабола. При r=R → v=0. При r=0 → V=Vmax=(P1-P2) / 4η·L
теперь выражение для объема жидкости Q, протекающей через поперечное сечение трубы за одну секунду.
За одну секунду, выделенный слой переносит объем жидкости, равный:
где dS - площадь заштрихованного кольца. Подставим сюда полученное ранее выражение для скорости:
Проинтегрируем получившееся уравнение:
Окончательно получим:
Это и есть формула Пуазейля (1799 – 1869), которая описывает объемный расход жидкости через круглую трубу, при ламинарном течении.

