Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К' (с координатами x', y', z'), движущуюся относительно К равномерно и прямолинейно со скоростью υ0 (υ0=const)
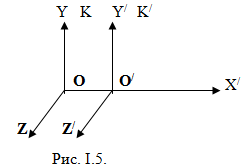
Координата точки А по отношению к системе К: х = х' + 00', за промежуток времени t от начала отсчета будет:
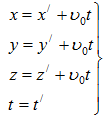(3.19)
Уравнения (3.19) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ'+υ0 (3.20)
Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a' (3.21), т.е. из соотношения (3.21) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.