Из третьего закона Ньютона следует, что в любой механической системе геометрическая сумма всех внутренних сил равна нулю:
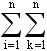 Fik=0
Fik=0где n – число материальных точек в системе, а Fii=0.
Центром масс (или центром инерции) системы материальных точек называется точка С, радиус-вектор которой равен:
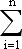 miri (2.5)
miri (2.5) где mi и ri – масса и радиус-вектор i-й материальной точки, а m=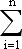 mi – масса всей системы.
mi – масса всей системы.
Скорость центра масс определяется как производная радиуса-вектора (2.5)
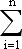 mivi=(1/m)
mivi=(1/m)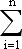 pi (2.6)
pi (2.6)Геометрическая сумма импульсов всех материальных точек системы в правой части выражения (2.6) называется импульсом системы p. Очевидно, что p=vmc. Из второго и третьего законов Ньютона следует, что первая производная импульса системы по времени равна главному вектору всех внешних сил, приложенных к системе:
Это уравнение выражает закон изменения импульса системы. На основании его можно сформулировать закон движения центра масс механической системы:
Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
Математическая запись этого закона имеет вид:
(d/dt)*mvc=Fвнеш, или mac=Fвнеш,
где ac – ускорение центра масс.
Если механическая система является замкнутой, т.е. главный вектор внешних сил равен нулю, то, очевидно,
Это и есть закон сохранения импульса замкнутой системы, являющийся одним из фундаментальных законов физики.
