или в виде:
где f(x), M(x),P(x) - некоторые функции переменной х; g(y), N(y), Q(y) - функции переменной у.
Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной х, окажутся в одной части равенства, а переменной у - в другой. Затем проинтегрируем обе части полученного равенства. Например, из (8) следует, что dy/g(y)=f(x)dx и 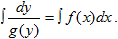 . Выполняя интегрирование, приходим к решению уравнения (8).
. Выполняя интегрирование, приходим к решению уравнения (8).
Пример 2. Решить уравнение √y2+1=dxdy
Разделив левую и правую часть уравнения на выражение x√y2+1 (при х≠0), приходим к равенству 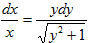 . Интегрируя, получим
. Интегрируя, получим 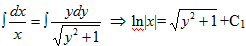 , (так как интеграл в левой части табличный, а интеграл в правой части может быть найден, например, заменой √y2+1=t, 2ydy=2tdt и
, (так как интеграл в левой части табличный, а интеграл в правой части может быть найден, например, заменой √y2+1=t, 2ydy=2tdt и 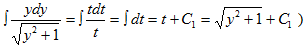
Решение перепишем в виде ±ec1e√y2+1 или x=Ce√y2+1, где C=±ec1
Пример 3. Решить уравнение y'=y/x
Разделяя переменные, получаем: dy/y=dx/x. Интегрируя имеем 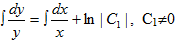 или ln|y|=ln|x|+ln|C1|. Потенцируя, находим |y|=|C1||x|, что эквивалентно уравнению y=±C1x. Полагая ±С1=С, окончательно получаем у=Сх - общее решение данного уравнения, где С - произвольная постоянная, отличная от нуля которая может принимать как положительные, так и отрицательные значения, но С≠0. Заметим, что у=0 также решение уравнения (оно было потеряно при делении на у). Это решение можно включить, если считать, что постоянная С принимает и значение С=0.
или ln|y|=ln|x|+ln|C1|. Потенцируя, находим |y|=|C1||x|, что эквивалентно уравнению y=±C1x. Полагая ±С1=С, окончательно получаем у=Сх - общее решение данного уравнения, где С - произвольная постоянная, отличная от нуля которая может принимать как положительные, так и отрицательные значения, но С≠0. Заметим, что у=0 также решение уравнения (оно было потеряно при делении на у). Это решение можно включить, если считать, что постоянная С принимает и значение С=0.
Пусть требуется выделить из общего решения частное решение, удовлетворяющее следующим начальным условиям: х0=1, у0=2. Подставляя эти значения в общее решение вместо х и у, получаем 2=C•1, откуда С=2. Таким образом , искомое частное решение y=2x.
Пример 4. Найти общее решение дифференциального уравнения (xy+y)dx+(xy+x)dy=0
Предположив, что x≠0, y≠0 и разделив обе части данного уравнения на xy получим уравнение с разделенными переменными 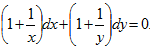 . Интегрируя его, последовательно находим (произвольную постоянную можно представить в виде ln|C|:
. Интегрируя его, последовательно находим (произвольную постоянную можно представить в виде ln|C|:
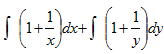 =ln|C|, ⇒ x+ln|x|+y+ln|y|=ln|C|, ⇒ ln|xy|+lnex+y=ln|C|, ⇒ xyex+y=C
=ln|C|, ⇒ x+ln|x|+y+ln|y|=ln|C|, ⇒ ln|xy|+lnex+y=ln|C|, ⇒ xyex+y=C
Последнее равенство является общим интегралом заданного дифференциального уравнения. При его нахождении были приняты ограничения x≠0, y≠0. Однако функции x=0, y=0 также является решениями исходного уравнения ,что легко проверяется; с другой стороны, они получаются из общего интеграла при С=0. Следовательно, x=0, y=0 частные решения исходного уравнения.
Пример 5. Найти частное решение уравнения (1+e2x)y2y'=ex, удовлетворяющее начальному условию y(0)=1
Запишем данное уравнение в дифференциальной форме: (1+e2x)y2dy-exdx=0. Теперь разделим переменные: y2dy-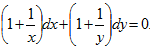 dx=0 Проинтегрируем последнее уравнение:
dx=0 Проинтегрируем последнее уравнение:
dy-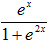
Получили общее решение исходного уравнения. Использовав начальное условие, определим значение произвольной постоянной: dy-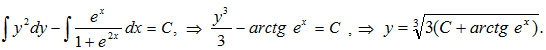
Следовательно, частное решение исходного уравнения имеет вид dy-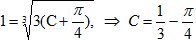 .
.
