Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких - то уравнением в частных производных.
Например, уравнение 2xy'-3y=0', где y=y(x), является обыкновенным дифференциальным уравнением первого порядка, а u'x-u'y+1=0, где u=u(x,y), дифференциальным уравнением в частных производных первого порядка.
Мы будем рассматривать только обыкновенные дифференциальные уравнения (и по этой причине само слово «обыкновенные» будет опускаться).
В общем случае дифференциальное уравнение можно записать в виде:
где F - некоторая функция от n+2 переменных, n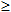 1, при этом порядок n старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения. Например, задача о нахождении первообразной приводит к дифференциальному уравнению первого порядка, уравнение x2(y''')4-x(y')5+8=0 третьего порядка и т.д.
1, при этом порядок n старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения. Например, задача о нахождении первообразной приводит к дифференциальному уравнению первого порядка, уравнение x2(y''')4-x(y')5+8=0 третьего порядка и т.д.
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение n-го порядка называется разрешенным относительно старшей производной, если оно имеет вид:
где F –некоторая функция от n+1 переменной.
ОПРЕДЕЛЕНИЕ. Решением дифференциального уравнения (1) называется такая функция y=y(x), которая при подстановке её в это уравнение обращает его в тождество. Например, функция y=sinx является решением уравнения y''+y=0, так как (sinx)''+sinx=0 для любых х.
ОПРЕДЕЛЕНИЕ. Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
Пример 1. Решить уравнение у''=х.
Поскольку y''=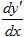 , то исходное уравнение равносильно следующему равенству дифференциалов: dy'=xdx. Выполняя почленное интегрирование, получаем y'=
, то исходное уравнение равносильно следующему равенству дифференциалов: dy'=xdx. Выполняя почленное интегрирование, получаем y'=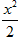 +C1, где C1 произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству dy=(
+C1, где C1 произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству dy=(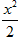 +C1)dx. Интегрируя почленно, окончательно получаем y=
+C1)dx. Интегрируя почленно, окончательно получаем y=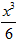 +C1x+C2, где C1 - произвольная постоянная.
+C1x+C2, где C1 - произвольная постоянная.
ОПРЕДЕЛЕНИЕ. Общим решением дифференциального уравнения (1) n-го порядка называется такое решение:
которое является функцией переменной x и n произвольных независимых постоянных C1,C2,…,Cn. (Независимость постоянных означает отсутствие каких - либо соотношений между ними). Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных C1,C2,…,Cn.
В примере 1 y=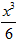 +C1x+C2 - общее решение, y=
+C1x+C2 - общее решение, y=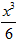 +2x+1 - частное решение дифференциального уравнения у''=х.
+2x+1 - частное решение дифференциального уравнения у''=х.
