Суть метода Жордана-Гаусса состоит в приведении системы (1) к ступенчатому виду.
Допустим, что в системе (1) коэффициент при первом неизвестном a₁₁≠0. Исключим сначала неизвестное x₁ из всех уравнений системы (1), кроме первого Для этого прежде всего разделим обе части первого уравнения на коэффициент a₁₁≠0, тогда получим новую систему, равносильную данной системе. Умножим теперь первое уравнение полученной системы на a₂₁ и вычтем из второго уравнения. Затем умножим первое уравнение на a₃₁ и вычтем из третьего уравнения и т.д. В результате получим новую систему, также равносильную данной системе.

Разделим теперь второе уравнение полученной системы на первый коэффициент, затем умножим второе уравнение полученной системы последовательно на коэффициенты остальных уравнений и вычтем поочередно из соответствующих уравнений системы, кроме первого и второго. Продолжая этот процесс, мы придем к системе – треугольной.

В случае треугольной системы из последнего уравнения находим x_n=b_n затем, подставляя значение x_n в предыдущее уравнение, находим x_n-1 и т.д.

На каком-то шаге исключения неизвестных может появиться уравнение вида 0•x₁+0•x₂+...+0•x_n, которому удовлетворяет любая совокупность чисел (x₁,x₂,...,x_n). Поэтому такое уравнение можно отбросить.

Может появиться такое уравнение вида  0•x₁+0•x₂+...+0•x_n=b, где b≠0, которому не удовлетворяет ни одна из совокупностей чисел (x₁,x₂,...,x_n). Это означает, что последнее уравнение, а вместе с ним и исходная система, решений не имеют, то есть система несовместна.

Если уравнение последнего вида не появляется ни на каком шаге и процесс исключения остановился, то число уравнений будет или равно, или меньше числа неизвестных. В случае, когда число уравнений равно числу неизвестных, система совместна и имеет единственное решение. Если же число уравнений меньше числа неизвестных, то система совместна и имеет бесконечно много решений. При этом выбираются базисные неизвестные, равные по количеству числу уравнений остальные неизвестные, называемые свободными, переносят в правые части всех уравнений. Придавая свободным переменным произвольные значения, находят значения базисных переменных через свободные.

Пример 3: Решить систему уравнений методом Жордана-Гаусса:

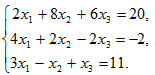
Разделив 1-ю строку на 2, получим

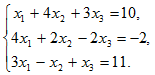
Исключим теперь члены с х₁ из 2-го и 3-го уравнений, вычитая из 2-й строки 1-ю, умноженную на 4, а из 3-й – 1-ю, умноженную на 3. Это дает

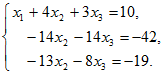
Разделим 2-ю и 3-ю строки соответственно на –14 и –1:

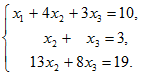
Умножим 2-ю строку на 13 и вычтем из 3-й:

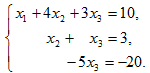
Разделим, наконец, 3-ю строку на –5:

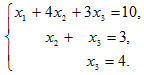
Тогда решением является x₃=4, x₂=3, x₃=-1,x₁=10-4x₂-3x₃=2

Здесь имеет место случай, когда число уравнений равно числу неизвестных, и решение единственно.