Системы линейных уравнений
Общей линейной системой из m уравнений с n неизвестными называется система:
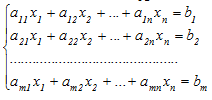
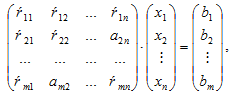 ,
,
где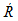 – матрица системы, X - вектор-столбец неизвестных коэффициентов, B - вектор-столбец свободных членов.
– матрица системы, X - вектор-столбец неизвестных коэффициентов, B - вектор-столбец свободных членов.
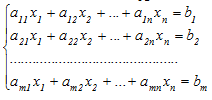
Данная запись эквивалентна матричной форме записи 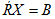
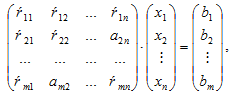 ,
,где
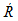 – матрица системы, X - вектор-столбец неизвестных коэффициентов, B - вектор-столбец свободных членов.
– матрица системы, X - вектор-столбец неизвестных коэффициентов, B - вектор-столбец свободных членов. Систему называют однородной, если b1=b2=…=bm=0.В противном случае ее называют неоднородной.
Системы уравнений классифицируются следующим образом:
1) несовместная система уравнений (нет решений),
2) совместная система уравнений (есть хотя бы одно решение):
a) определенная (только одно решение),
b) неопределенная (бесконечно много решений).
Одной из основных является следующая теорема.
Теорема (Кронекера-Капелли)
Пусть 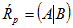 - расширенная матрица системы (1).
- расширенная матрица системы (1).
1) Система (1) совместна 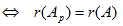
a) если 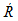 - матрица размера n x n, причем
- матрица размера n x n, причем 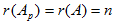 , то система определенная.
, то система определенная.
b) если 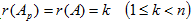 , то система неопределенная.
, то система неопределенная.
2) Если 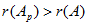 , то система несовместная.
, то система несовместная.
Поиск на сайте
