Пусть у нас имеются n серии значений двух параметров X и Y: (x₁;y₁),(x₂;y₂),...,(x_n;y_n). Подразумевается, что у одного и того же объекта измерены два параметра. Нам надо выяснить есть ли значимая связь между этими параметрами.

Как известно, случайные величины X и Y могут быть либо зависимыми, либо независимыми. Существуют следующие формы зависимости – функциональная и статистическая. В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y=f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Однако, если X и Y случайные величины, то между ними может существовать зависимость иного рода, называемая статистической. Дело в том, что на формирование значений случайных величин X и Y оказывают влияние различные факторы. Под воздействием этих факторов и формируются конкретные значения X и Y. Допустим, что на Х и У влияют одни те же факторы, например Z₁, Z₂, Z₃, тогда X и Y находятся в полном соответствии друг с другом и связаны функционально. Предположим теперь, что на X воздействуют факторы Z₁, Z₂, Z₃, а на только Y и Z₁, Z₂. Обе величины и X и Y являются случайными, но так как имеются общие факторы Z₁ и Z₂, оказывающие влияние и на X и на Y, то значения X и Y обязательно будут взаимосвязаны. И связь это уже не будет функциональной: фактор Z₃, влияющий лишь на одну из случайных величин, разрушает прямую (функциональную) зависимость между значениями X и Y, принимаемыми в одном и том же испытании. Связь носит вероятностный случайный характер, в численном выражении меняясь, от испытания к испытанию, но эта связь определенно присутствует и называется статистической. При этом каждому значению X может соответствовать не одно значение Y, как при функциональной зависимости, а целое множество значений.

ОПРЕДЕЛЕНИЕ. Зависимость случайных величин называют статистической, если изменения одной из них приводит к изменению закона распределения другой.

ОПРЕДЕЛЕНИЕ. Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные коррреляционной зависимостью, оказываются коррелированными.

Примерами коррреляционной зависимости являются: зависимость массы от роста:
- каждому значению роста (X) соответствует множество значений массы (Y), причем, несмотря на общую тенденцию, справедливую для средних, большему значению роста соответствует и большее значение массы – в отдельных наблюдениях субъект с большим ростом может иметь и меньшую массу.
- зависимость заболеваемости от воздействия внешних факторов, например, запыленности, уровня радиации, солнечной активности и т.д.
- количество (X) вводимого объекту препарата и его концентрация в крови (Y).
- между показателями уровня жизни населения и процентом смертности;
- между количеством пропущенных студентами лекций и оценкой на экзамене.
Именно корреляционные зависимости наиболее часто встречаются в природе в силу взаимовлияния и тесного переплетения огромного множества самых различных факторов, определяющих значения изучаемых показателей.

Корреляционную зависимость Y от X можно описать с помощью уравнения вида:

где y_x - условное среднее величины Y, соответствующее значению x величины X, а f(x) некоторая функция. Уравнение (1) называется выборочным уравнением регрессии Y на X. Функцию f(x) называют выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X.

Совершенно аналогично выборочным уравнением регрессии X на Y является уравнение: x_y=φ(y)

В зависимости от вида уравнения регрессии и формы соответствующей линии регрессии определяют форму корреляционнной зависимости между рассматриваемыми величинами – линейной, квадратической, показательной, экспоненциальной.

Важнейшим является вопрос выбора вида функции регрессии f(x) [или φ(y)], например линейная или нелинейная (показательная, логарифимическая и т.д.)

На практике вид функции регрессии можно определить, построив на координатной плоскости множество точек, соответствующих всем имеющимся парам наблюдений (x;y).

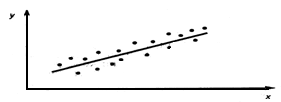
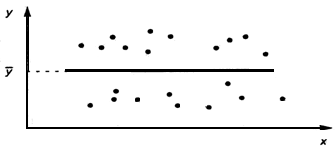
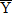
Например, на рис.1. видна тенденция роста значений Y с ростом X, при этом средние значения Y располагается визуально на прямой. Имеет смысл использовать линейную модель (вид зависимости Y от X принято называть моделью) зависимости Y от X. На рис.2. средние значения Y не зависят от x, следовательно линейная регрессия незначима (функция регрессии постоянна и равна 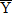). На рис. 3. прослеживается тенденция нелинейности модели.