| Модератор форума: Bukashka, noka |
| Форум "Казахстан и образование"Математика геометрия Ученический форум Математика Тригонометрические уравнения (Решение тригонометрических уравнений,частные случаи, формулы) |
| Тригонометрические уравнения |
Гость
23.03.2012, 22:49, Пятница | Сообщение 121
Решите пожалуйста cosx=sin2x
|
|
23.03.2012, 22:53, Пятница | Сообщение 122
Quote (Гость) Решите пожалуйста cosx=sin2x sin2x=2sinxcosx 2sinxcosx-cosx=0 cosx(2sinx-1)=0 1.cosx=0 x=π/2+πn 2.sinx=1/2 x=(-1)^k*π/6+πn |
Гость
24.03.2012, 10:57, Суббота | Сообщение 123
Как такое решать? Объясните! ctg(p/2+arctg3)
|
|
24.03.2012, 13:23, Суббота | Сообщение 124
Quote (Гость) Как такое решать? Объясните! ctg(p/2+arctg3) ctg(π/2+arctg3) там стоить π/2 поэтому ctg меняется на tg(есть такое правила) станет вот так -tgarctg3 стоит минус потому что ctg во втором - тогда ответ будет -3 -tgarctg3=-3 |
Гость
24.03.2012, 13:53, Суббота | Сообщение 125
Спасибо огромное! И еще одно задание у меня не получается( tgA=4/3 tgB=1/4 Найти tgA+B |
|
24.03.2012, 14:05, Суббота | Сообщение 126
Quote (Гость) Спасибо огромное! И еще одно задание у меня не получается( tgA=4/3 tgB=1/4 Найти tgA+B Найти tg(A+B) это так? Добавлено (24.03.2012, 13:05) Добавлено (24.03.2012, 13:05) |
|
24.03.2012, 23:36, Суббота | Сообщение 127
sin15*cos7 - сos 11cos79
|
|
24.03.2012, 23:42, Суббота | Сообщение 128
Quote (Lonely_MooN2055) sin15*cos7 - сos 11cos79 sin15*cos7=1/2(sin8+sin22) cos11cos79=sin79cos79=1/2sin158=1/2sin22 (sin8+sin22-sin22)/2=1/2sin8 |
Гость
25.03.2012, 19:04, Воскресенье | Сообщение 129
tga+ctga=m, tg^2a+ctg^2a...prowu pomogite..budu blagodarna
|
|
25.03.2012, 20:02, Воскресенье | Сообщение 130
Quote (Гость) tga+ctga=m, tg^2a+ctg^2a...prowu pomogite..budu blagodarna (Tga+ctga)^=m^2 tg^2a+ctg^2a+2tgactga=m^2 tg^2a+ctg^2a=m^2-2 |
|
26.03.2012, 17:09, Понедельник | Сообщение 131
не уравнение, но все таки помогите пожалуйста. Я так прикинул вроде единица будет. 
|
|
26.03.2012, 17:19, Понедельник | Сообщение 132
 Первое упростить второе вычислить |
|
26.03.2012, 17:23, Понедельник | Сообщение 133
Еще одно только с плюсом, тоже вычислить  ps кто может сделайте одно сообщение |
|
26.03.2012, 17:31, Понедельник | Сообщение 134
Damir0087, что такое cot?
|
|
26.03.2012, 17:43, Понедельник | Сообщение 135
noka, катангенс, tan- тангенс Добавлено (26.03.2012, 16:43) |
|
26.03.2012, 18:30, Понедельник | Сообщение 136
помогите вот с этой задачей 1+sin2x = cosx+sinx в ответе должно выйти: -pi/4+pin, pi/2+2pin; 2pin; у меня выходит только 2 из этих трех Добавлено (26.03.2012, 17:29) Добавлено (26.03.2012, 17:30) |
|
27.03.2012, 10:46, Вторник | Сообщение 137
Те два сделал осталось только это, может кто поможет пожалуйста. cot-котангенс, tan - тангенс 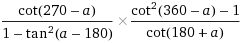
|
|
27.03.2012, 10:57, Вторник | Сообщение 138
Quote (Damir0087) Те два сделал осталось только это, может кто поможет пожалуйста. cot-котангенс, tan - тангенс tga/(1-tg^2a)*(ctg^2a-1)/ctga= sina/cosa/(cos^2a-sin^2a)/cos^2a*(cos^2a-sin^2a)/sin^2a/sina/cosa= sinacosa/(cos^2a-sin^2a)* (cos^2a-sin^2a)/sinacosa=1 |
|
28.03.2012, 00:14, Среда | Сообщение 139
2sinΛ2(x-п/4) = 2sinΛ2x- tgxДобавлено (27.03.2012, 23:14) |
|
28.03.2012, 03:26, Среда | Сообщение 140
Lonely_MooN2055, по формуле понижения степени не пробовала?щас уже поздно ,завтра на свежую голову посмотрю)
|
|
28.03.2012, 09:17, Среда | Сообщение 141
правильный ответ +-П/4+Пк
|
|
28.03.2012, 13:43, Среда | Сообщение 142
2sinΛ2(x-п/4) = 2sinΛ2x- tgx Понижаем степень 1-cos(2x-π/2)=1-cos2x-tgx 1-sin2x=1-cos2x-tgx-я вот здесь ошибся в 90 градусов соs меняется на синус же sin2x-cos2x-tgx=0 2sinxcosx-cos^2x+sin^2x-sinx/cosx=0 2sinxcos^2x-cos^3x+sin^2xcosx-sinx=0 2sinx(1-sin^2x)-cos^3x+cosx(1-cos^2x)-sinx=0 2sinx-2sin^3x-cos^3x+cosx-cos^3x-sinx= sinx-2sin^3x+cosx-2cos^3x=0 sinx(1-2sin^2x)+cosx(1-2cos^2x)=0 sinxcos2x-cosxcos^2x=0 cos2x(sinx-cosx)=0 1.cos2x=0 2x=π/2 x=π/4 2.sinx=cosx tgx=1 x=π/4+πn |
|
28.03.2012, 15:28, Среда | Сообщение 143
вот я решила так 2sin2(x-π/4) = 2sin2x- tgx 1-cos(2x-π/2)=1-cos2x-tgx sin2x-cos2x-tgx=0 2sinx*cosx-cos2x+sin2x=tgx cos2x(2tgx-1+tg2x)=tgx 2tgx-1+tg2x=tgx(1+tg2x) 2tgx-1+tg2x=tgx+tg3x tg3x-tg2x-tgx+1=0 tg2x(tgx-1)-(tgx-1)=0 (tgx-1)(tg2x-1)=0 1) tgx-1=0 tgx=1 x1=π/4+πn 2)tg2x-1=0 tg2x=1 tgx=±1 tgx=-1 x2=-π/4+πn |
|
28.03.2012, 17:51, Среда | Сообщение 144
Noka рещи плз! 
|
|
28.03.2012, 21:08, Среда | Сообщение 145
Довольно тривиальная задача на знание тригонометрических тождеств и ФСУ: Решение: 1*) Простые преобразования, доводим выражение в скобках до полного квадрата: 2(sin^4(x) + sin^2(x)cos^2(x) + cos^4(x))^2 - sin^8(x) - cos^8(x) 2(sin^4(x) + 2sin^2(x)cos^2(x) - sin^2(x)cos^2(x))^2 - sin^8(x) - cos^8(x) 2((sin^2(x) + cos^2(x))^2 - sin^2(x)cos^2(x))^2 - sin^8(x) - cos^8(x) 2*) sin^2(x) + cos^2(x) = 1 - основное тождество. 2((1)^2 - sin^2(x)cos^2(x))^2 - sin^8(x) - cos^8(x) 2(1 - sin^2(x)cos^2(x))^2 - sin^8(x) - cos^8x 3*) Раскрываем квадрат: 2(1 - 2sin^2(x)cos^2(x) + sin^4(x)cos^4(x)) - sin^8(x) - cos^8(x) 2 - 4sin^2(x)cos^2(x) + 2sin^4(x)cos^4(x) - sin^8(x) - cos^8(x) 4*) Опять составляем полный квадрат: от 2sin^4(x)cos^4(x) - sin^8(x) - cos^8(x) 2 - 4sin^2(x)cos^2(x) - (cos^8(x) - 2sin^4(x)cos^4(x) + sin^8(x)) 2 - 4sin^2(x)cos^2(x) - (cos^4(x) - sin^4(x))^2 5*) cos^4(x) - sin^4(x) - есть формула двойного угла косинуса cos2x. Доказательство: cos^2(x)cos^2(x) - sin^2(x)sin^2(x) cos^2(x)(1-sin^2(x)) - sin^2(x)sin^2(x) cos^2(x) - cos^2(x)sin^2(x) - sin^2(x)sin^2(x) cos^2(x) - sin^2(x)(cos^2(x) + sin^2(x)) cos^2(x) - sin^2(x)*(1) = cos2x Доказано. Возвращаемся к примеру: 2 - 4sin^2(x)cos^2(x) - (cos^4(x) - sin^4(x))^2 2 - 4sin^2(x)cos^2(x) - (cos2x)^2 2 - 4sin^2(x)cos^2(x) - cos^2(2x) 6*) используем формулы понижения для избавления от квадратов в функциях sin^2(x),cos^2(x) sin^2(x) = (1 - cos2x)/2 cos^2(x) = (1 + cos2x)/2 2 - (4(1 - cos2x)(1+cos2x))/4 - cos^2(2x) 2 - (1-cos2x)(1+cos2x) - cos^2(2x) 2 - (1 - cos^2(2x)) - cos^2(2x) 2 - 1 + cos^2(2x) - cos^2(2x) Косинусы уходят остаётся: 2 - 1 = 1 Это и есть ответ к твоей задаче. Это было фул решение, но можно поступить гораздо проще просто заместо x поставить какой-нить будь угол например Pi/4. Получится: 2(sin^4(pi/4) + sin^2(pi/4)cos^2(pi/4) + cos^4(pi/4))^2 - sin^8(pi/4) - cos^8(pi/4) 2(1/4 + 1/4 + 1/4)^2 - 1/16 - 1/16 2*(9/16) - 1/16 - 1/16 9/8 - 1/16 - 1/16 = 1 Как видите решается намного быстрее, но рекомендую на пробных так не халявить. |
|
28.03.2012, 23:37, Среда | Сообщение 146
noka, lда. мы пришли к третьей степени,только через универсальную подстановку..) значит это реально непростое уравнение |
|
28.03.2012, 23:41, Среда | Сообщение 147
Lonely_MooN2055, значит непростое))
|
Гость
29.03.2012, 20:11, Четверг | Сообщение 148
2sin(3x/2)cos(3x/2)-sin^2 3x=0
|
Гость
29.03.2012, 20:17, Четверг | Сообщение 149
Помогите решить пожалуйста: 6cos^2x+5cos(пи/2-x)=7? Заранее спасибки!!!
|
|
29.03.2012, 20:21, Четверг | Сообщение 150
Quote (Гость) 2sin(3x/2)cos(3x/2)-sin^2 3x=0 sin3x-sin^23x=0 -sin3x(sin3x-1)=0 1.sin3x=0 3x=πk x=πk/3 2.sin3x=1 3x=π/2+2πn x=π/6+2πn/3 Добавлено (29.03.2012, 19:21) Quote (Гость) Помогите решить пожалуйста: 6cos^2x+5cos(пи/2-x)=7? Заранее спасибки!!! 6cos^2x+5sinx=7 6-6sin^2x+5sinx=7 6sin^2x-5sinx+1=0 sinx=t 6t^2-5t+1=0 D=1 t=5+1=6/12=1/2 t=5-1=4/12=1/3 1.sinx=1/2 x=(-1)^k π/6+πn 2.sinx=1/3 x=arcsin1/3+πn |
| |||
 Друзья сайта
Друзья сайта Студенты
Студенты Ученики
Ученики
 Заблокированные
Заблокированные