ОБОРУДОВАНИЕ: набор капилляров, стеклянный баллон, насос, манометр, барометр, секундомер.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Явление переноса – это процесс установления равновесия в системе путём переноса массы (диффузия), энергии (теплопроводности) и импульса молекул (внутреннее трение или динамическая вязкость).
Эти явления происходят в неравновесном состоянии, т.е. при наличии в системе градиентов плотности dρ / dx, температуры dT/dx и скорости частиц du/dx, обусловлены тепловым движением молекул.
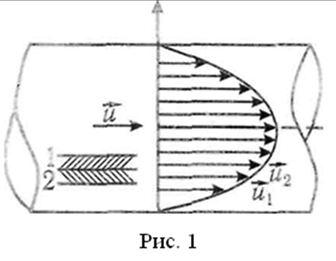
В явлении вязкости наблюдается перенос импульса от более быстрых участков потока к менее быстрым. При течении газа или жидкости, например внутри трубы, скорости слоев различны: их распределение при ламинарном течении показано на рис. 1 (длина стрелки показывает скорость данного слоя). Причиной этого является хаотическое тепловое движение молекул, при котором они непрерывно переходят из слоя в слой и в соударениях с другими молекулами обмениваются импульсами. Так, молекулы второго слоя, попадая в слой 1, переносят свой импульс направленного движения m0u2, а в слой 2 приходит молекулы с меньшим импульсом m0u1. В результате второй слой тормозится, а первый – ускоряется. Опыт показывает, что импульс dp, передаваемый от слоя к слою через поверхность S, пропорционален градиенту скорости du/dx, площади S и времени переноса dt:
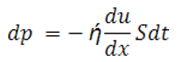
В результате между слоями возникает сила внутреннего трения (закон Ньютона):
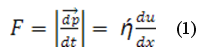
где
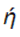– коэффициент вязкости среды. Для идеального газа коэффициент вязкости:
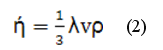
Средняя длина свободного пробега молекул:
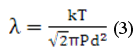
где k = 1.38∙10-23 Дж/K – постоянная Больцмана,
d – эффективный диаметр молекул (для воздуха d≈4∙10-10 м)
T, P – температура и давление газа.
Средняя скорость теплового движения молекул:
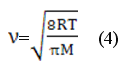
где R = 8.31 Дж/моль∙К – универсальная газовая постоянная,
М – масса одного моля газа (для воздуха М = 28,9 г/моль).
Плотность газа согласно уравнению состояния идеального газа:
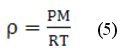
При ламинарном течении через трубку круглого сечения радиусом r (капилляр) и длиной L за время t протекает газ или жидкость, объем V которых определяется по формуле Пуазейля:
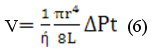
где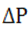 
- разность давлений на концах капилляра.
Поток тепла dQ/dt, переносимого через поверхность S, нормальную потоку, зависит от градиента температуры dT/dx в направлении переноса (закон Фурье):
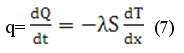
где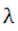 
- коэффициент теплопроводности, для идеального газа:
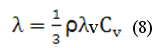
Здесь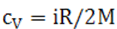 
- удельная теплоемкость газа при постоянном давление, i – число степеней свободы молекулы газа.
ОПИСАНИЕ УСТАНОВКИ
Установка состоит из баллона Б, жидкостного манометра М и набора капилляров (1-5), соединенных с баллоном кранами (К1- К5). давление воздуха в баллоне до необходимого можно повысить с помощью компрессора при открытом кране К и закрытых кранах (К1-К5) и К0. Кран К0 используется для практически мгновенного выпускания воздуха из баллона.
В установках капилляры соединены либо параллельно различного сечения (рис. 1), либо последовательно (рис.2) одинакового сечения. Если при закрытых кранах К и Ко открыть кран К1 (при закрытых кранах К2-К5), то воздух из баллона будет вытекать через первый капилляр. Если открыть кран К2 (при закрытых кранах К1, К3, К4 и К5), то воздух будет вытекать через второй капилляр и т.д.
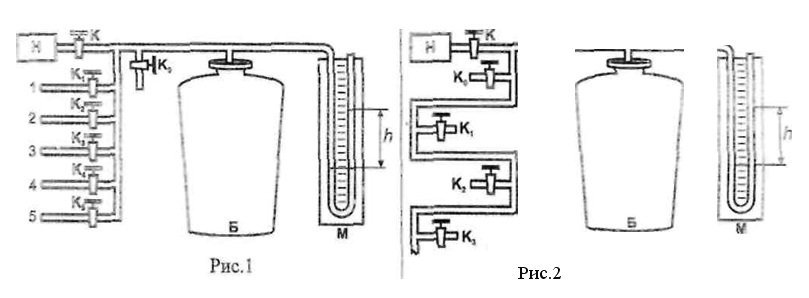
В установке другого типа (рис. 2) при открытом кране К1 воздух вытекает через первый капилляр, при открытом кране К2 воздух вытекает через два последовательно соединенных капилляра 1 и 2, что эквивалентно вытеканию воз¬духа через капилляр длиной, равной сумме длин двух капилляров l1 + l2.
А если открыть кран К5, то воздух будет вытекать через последовательно соединенные 5 капилляров или капилляр, имеющий длину l1 +l2 +l3 +l4 +l5
Примечание: сечение соединительных трубок много больше сечения капилляра и их сопротивление практически равно нулю, т.к. сопротивление пропорционально r4 (формула Пуазейля 6).
