Суммой двух матриц A=(a_ij) и B=(b_ij) с одинаковым количеством m строк и n столбцов называется матрица C=(cij), элементы которой определяются равенством a_ij+b_ij=c_ij(i=1,2...,m; j==1,2...,n;).

Обозначим: А+В=С.

Пример 2: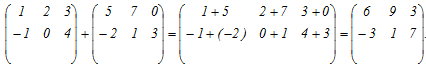

Аналогично определятся разность двух матриц.

Произведением матрицы A=(aij) на число 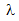называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число :
.

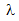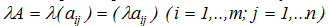Пример 3: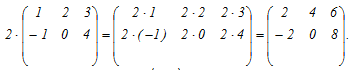

Произведением матрицы A=(a_ij), имеющей m строк и k столбцов, на матрицу B=(b_ij), имеющую k строк и n столбцов, называется матрица C=(c_ij), имеющая m строк и n столбцов, у которой элемент c_ij равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В, т.е. c_ij=a_i1b_1j+a_i2b_2j+....+a_ikb_kj (i=1,2...,m; j==1,2...,n;)

При этом число k столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено.

Произведение обозначается так: AB=C

Пример 4: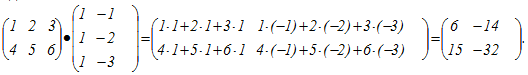

Пример 5: Пусть 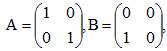, тогда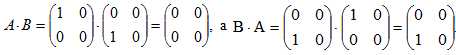

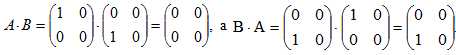
Отсюда получаем, что АВ≠ВА, т.е. умножение матриц не обладает перестановочным свойством.

Для суммы и произведения матриц справедливы следующие соотношения:

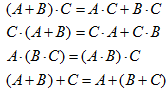
Умножение на единичную матрицу.

Совокупность элементов a₁₁,a₂₂,...,a_nm квадратной матрицы A=(a_ij) называется главной диагональю матрицы.

Единичной матрицей называется матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны нулю. Обозначается единичная матрица буквой Е.

Например 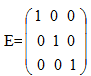- единичная матрица третьего порядка.
Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Пример 6: Пусть 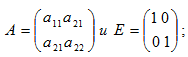, тогда согласно правилу умножения матриц имеем 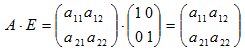и ,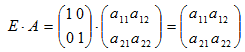
Откуда А•Е=А и Е•А=А.