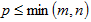, m,n,p- натуральные числа. Введем следующие понятия:
Минор p-го порядка – это определитель, составленный из элементов матрицы А, стоящих на пересечении выбранных p-строк и p-столбцов.
Ранг матрицы A (rA) равен наибольшему порядку отличных от нуля миноров этой матрицы. Если равны нулю все определители порядка k, порожденные данной матрицей A, то rA<k.
Базисный минор матрицы А – это отличный от нуля минор этой матрицы, порядок которого равен рангу матрицы А.
Теорема. Ранг матрицы не меняется при элементарных преобразованиях матрицы, под которыми подразумевается следующее:
1) Вычеркивание строки (столбца) все элементы которой равны нулю.
2) Перестановка строк (столбцов) матрицы.
3) Умножение строки (столбца) на ненулевое число.
4) Прибавление к одной из строк (столбцов) другой, умноженной на ненулевое число.
С помощью элементарных преобразований любую матрицу можно привести к виду, когда каждый ее ряд будет состоять только из нулей или из нулей и одной единицы. Тогда число оставшихся единиц и определяет ранг исходной матрицы, т.к. полученная матрица будет эквивалентна исходной.
