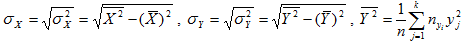На практике в результате независимых наблюдений над величинами X и Y, как правило, имеют дело не со всей совокупностью всех возможных пар значений этих величин, а лишь с ограниченной выборкой из генеральной совокупности, причем объем n выборочной совокупности определяется как количество имеющихся в выборке пар.

Первоочередной задачей статистической обработки экспериментального материала является систематизация полученных данных и выяснение формы соответствующей генеральной совокупности.

Пусть величина Х в выборке принимает значения x₁, x₂,....x_m, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y₁, y₂,....y_k, где k - количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.

Первым этапом статистической обработки результатов является составление корреляционной таблицы (таблица 1).

Y\X	x1	x2	...	xm	ny
y1	n12	n21		nm1	ny1
y2		n22		nm2	ny2
...
yk	n1k	n2k		nmk	nyk
nx	nx1	nx2		nxm	n

В первой строке основной части таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величины X. В первом столбце также в порядке возрастания перечисляются все встречающиеся в выборке значения величины Y. На пересечении соответствующих строк и столбцов указываются частоты n_ij (i=1,2,...,m; j=1,2,...,k) равные количеству появлений пары (x_i;y_i) в выборке. Например, частота n₁₂ представляет собой количество появлений в выборке пары (x₁;y₁).

Так же n_xin_ij, 1≤i≤m, сумма элементов i-го столбца, n_yjn_ij, 1≤j≤k, - сумма элементов j-ой строки и n_xi=n_yj=n

Аналоги формул (3), полученные по данным корреляционной таблицы, имеют вид:

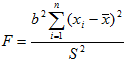(6)

Пример 3. Изучалась зависимость между качеством стандартности товаров Y(%) и количеством товаров (X) шт. Результаты наблюдений приведены в виде корреляционной таблицы.

Y\X	18	22	26	30	ny
70	5				5
75	7	46	1		54
80		29	72		101
85			29	8	37
90				3	3
nx	12	75	102	11	200

Требуется:
1) Найти выборочное уравнение прямой регрессии Y на X.
2) Определить выборочные аналоги функции регрессии.
3) Сравнить между собой при каждом значении Х приближения средних значений Y, полученные по функции регрессии и по уравнению прямой регрессии.

Решение: Пользуясь данными, приведенными в этой таблице, по формулам (6), находим:

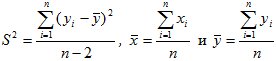
Следовательно,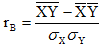
a=79.475-1.111•24.24=79.475-26.930=52.544

Таким образом, выборочное уравнение прямой регрессии Y на X выражается формулой:

Y=79.475+1.111(x-24.24)=79.475+1.111x-26.930=52.545+1.111x

Откуда:

X	18	22	26	30
Yлин	72.5	76.98	81.45	85.92
Yx	72.91	76.93	81.37	86.36

где Y_лин(x=x₁)=52.545+1.111•18=72.5 и т.д. y_x1=(5•70+7•75)/12=72.91 и т.д.

Сопоставляя полученные результаты, приходим к выводу, что значения, вычисленные по уравнению выборочной регрессии и по линейной зависимости хорошо согласуются.

Заключение. Величины, вычисленные путем подстановки возможных значений Х в уравнение прямой регрессии и в функцию регрессии, практически совпадают.

Замечание. Для упрощения вычислений в корреляционной табл. удобно от (x_i;y_i) перейти к новым переменным (u_i;v_i), положив u_i=(x_i-x₀)/h₁; v_j=(y_j-y₀)/h₂ (*)

где x₀ и y₀ варианты соответствующие наибольшим частотам соответственно x_i и y_i. h_i=x_i+1-x_i.

Обратный пересчет осуществляется по формулам: