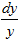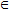ОПРЕДЕЛЕНИЕ: Функция f(x,y) называется однородной функцией измерения α относительно аргументов x и y, если равенство f(tx,ty)=t^αf(x,y) справедливо для любого tR при котором функция f(tx,ty) определена, α=const.

Например, функция f(x,y)=3x⁴-x²y²+5y⁴ является однородной четвертого измерения (α=4), так как f(tx,ty)=3(tx)⁴-(ty)²(tx)²+5(ty)⁴=t(3x⁴-x²y²+5y⁴)=t⁴f(x,y)

Функция f(x,y)= ³√x²-2³√xy+4³√y² является однородной измерения поскольку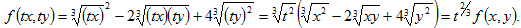

ОПРЕДЕЛЕНИЕ: Дифференциальное уравнение в форме

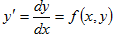
называется однородным относительно переменных х и у, если f(x,y) - однородная функция нулевого измерения относительно своих аргументов, т.е f(tx,ty)=t⁰f(x,y)=f(x,y)

Дифференциальное уравнение в форме

P(x,y)dx+Q(x,y)dy=0

будет однородным в том и только в том случае, когда P(x,y), Q(x,y) - однородные функции одного и того же измерения α т.е. P(tx,ty)=t^αP(x,t); Q(x,y)=t^αQ(x,t)

Однородное дифференциальное уравнение приводится к дифференциальному уравнению с разделяющимися переменными с помощью замены y=ux; y'=u'x+u.

Пример 6. Проинтегрировать дифференциальное уравнение 2x²y'=x²+y² и найти его частное решение, удовлетворяющее начальному условию у(1)=0.

Так как функции 2x² и x²+y² - однородные второго измерения, то данное уравнение – однородное. Сделаем замену y=ux; y'=u+xu'. Тогда 2x²(u+xu')=x²+(xu)² ⇒ 2x²(u+xu')=x²(1+u²)'

Предполагая, что x≠0, сокращаем обе части уравнения на x². Далее имеем 2u+2x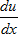=1+u² ⇒ 2xdu=(1+u²-2u)dx. Разделяя переменные, последовательно находим:

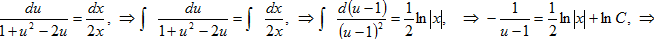1=(1-u)ln(C√|x|)

В последнее выражение вместо u подставим значение y/x. Получим общий интеграл:

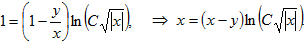
Разрешив его относительно у, найдем общее решение исходного дифференциального уравнения:

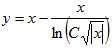
Использовав начальное условие у(1)=0, определим значение C:0=1-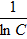 ⇒ lnC=1 ⇒ C=e

Следовательно, частное решение исходного уравнения имеет вид