Уравнением линии на плоскости в прямоугольной системе координат хОу называется уравнение f(х,у)=0, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.
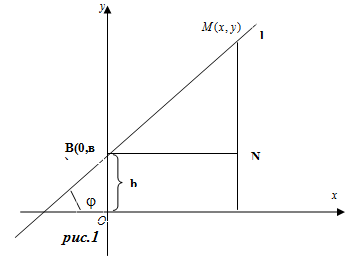
Пусть прямая l не параллельна оси Оу (рис.1). Обозначим точку пересечения прямой l с осью Оу буквой В(О;в), а угол между положительным направлением оси Ох и прямой l обозначим угол, отсчитываемый от оси Ох против часовой стрелки (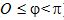
), называется углом наклона прямой l к оси Ох.
Выведем уравнение прямой l.
Пусть М(х,у) – произвольная точка прямой l с текущими координатами х,у. Из прямоугольного треугольника ВМN (рис.1) имеем:
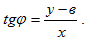(1)
Отсюда y-в=xtgφ, или у=xtgφ+в и окончательно
y=kx+в (2)
где k=tgφ - Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
Уравнение (2) называется уравнением прямой с угловым коэффициентом.
Число в – это величина отрезка, отсекаемого прямой на оси ординат.
Пример 1. Составить уравнение прямой линии, отсекающей на оси ординат отрезок, величина которого равна -2, и наклоненной к оси абсцисс под углом в 45°.
Решение. Здесь в=-2 и k=tg450=1. Следовательно, искомое уравнение y=x-2
Пример 2. Если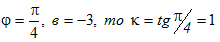 
и уравнение данной прямой имеет вид у=х-3.
Если в уравнении (2) к=0, то имеем уравнение прямой, параллельной оси Ох и проходящей через точку В(0;в):
у=в (3)
При в=0 из (8) получаем уравнение координатной оси Ох: у=0.
По аналогии с уравнением (3) уравнение
х=а (4)
есть уравнение прямой, параллельной оси Оу и проходящей через точку А(а;0). При а=0 из равенства (4) имеем уравнение координатной оси Оу: х=0.
