Условие параллельности прямых заключается в равенстве их угловых коэффициентов.

  tgφ₁=tgφ₂ или k₁=k₂

Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1

k₁k₂=-1

Пример 6. Проверить, выполняется ли условие параллельности прямых 2х-3у+1=0 и 4х-6у-5=0 ?

Решение: Угловые коэффициенты этих прямых 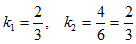, т.е. условие параллельности выполнено.

Пример 7. Составить уравнение прямой линии, проходящей через точку (1;2) параллельно прямой 2х-3у+1=0.

Решение. Угловой коэффициент k прямой линии, для которой нужно составить уравнение, равен угловому коэффициенту 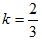данной прямой в силу условия параллельности этих прямых. Таким образом, 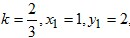получим искомое уравнение: 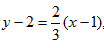или, умножая на 3: 3y-6=2(x-1), или 3y-6=2x-2, откуда окончательно находим: 2x-3y+4=0

Пример 8. При каком значении k уравнение y=kx+1 определяет прямую, перпендикулярную к прямой у=2х-1?

Решение: Угловой коэффициент второй прямой k₂=2. Условие перпендикулярности дает 2k=-1, откуда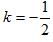

Пример 9. Составить уравнение прямой линии, проходящей через точку (-1;1) перпендикулярно к прямой 3х-у+2=0.

Решение: Искомый угловой коэффициент обозначим через k₁, угловой коэффициент данной прямой k₂, как видно из ее уравнения, равен 3. Условие перпендикулярности k₁k₂=-1 нам дает: 3k₁=-1, откуда 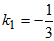. Таким образом, искомое уравнение 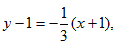, или 3у-3=-х-1, и окончательно x+3y-2=0