Свойства жидкостей и газов во многом отличаются, однако, в ряде механических явлений их поведения являются одинаковыми параметрами и идентичными уравнениями.

Поэтому гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействия между собой и обтекаемыми ими твердыми телами, - использует единый подход к изучению жидкостей и газов.

P=ΔF/ΔS - давление жидкости, [P]-1Па=1Н/м²;

Давление жидкости на дно и стенки сосуда P=ρgh называется гидростатическим. Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости. Течение жидкости называется установившимся (стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

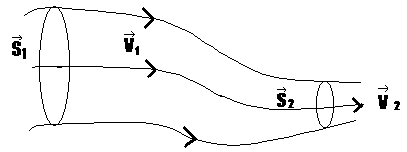
S₁V₁=S₂V₂=const (3.24) называется уравнением неразрывности для несжигаемой жидкости. Уравнение неразрывности означает, что через различные сечения трубки за одинаковый промежуток времени проходит одинаковое по объему количество жидкости. Т.е. чем меньше сечение трубки, скорость течения больше и наоборот. P=ρυ²/2 называется гидродинамическим давлением. Уравнение: ρυ²/2+ρgh₁+P₁=ρυ₂²/2+ρgh₂+P₂ (3.25) или ρυ²/2+ρgh+P=const (3.26) называется уравнением Бернулли. Для горизонтальной трубки тока выражение (3.26) примет вид: ρυ²/2+P=const (3.27), откуда следует, при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, я статическое давление больше в более широких местах, т.е. там, где скорость меньше. Этот вывод положен в основу работы водоструйного насоса.