Элементарной работой δA силы F на малом перемещении точки M приложения силы называется скалярное произведение F на dr:
где r и v=dr/dt – радиус-вектор и скорость точки M; dt – малый промежуток времени, в течение которого сила Fсовершает работу δA.
где ds=|dr| - путь точки M за малое время dt; α - угол между силой F и элементарным перемещением dr; Fs - проекция силы F на направление dr.
Из (3.1) видно, что работа под действием силы не совершается в двух случаях:
1) точка приложения силы неподвижна (dr=0);
2) α=±π/2, то есть F⊥v.

Рис.3.1. К определению понятия «работа силы»
Работа – величина аддитивная, это означает, что работа силы на участке траектории 1-2 равна алгебраической сумме элементарных работ на всех бесконечно малых участках пути. Эта сумма сводится к интегралу:
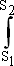 Fcosαds=
Fcosαds=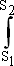 Fsds
FsdsЕсли зависимость Fs от пути S вдоль траектории 1-2 представить графически (рис.3.2), работа A определяется на графике как площадь заштрихованной фигуры.

Рис.3.2. Работа на участке траектории (S1, S2)
Единица работы – джоуль (Дж): 1 Дж – работа, совершаемая телом под действием силы 1 Н на пути 1 м (1 Дж = 1 Н•м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
За время dt сила F совершает работу Fdr, и мощность, развиваемая телом под действием этой силы в данный момент времени:
Мощность – величина скалярная; единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт =1 Дж/с).
