Работа δA силы T на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dt тела, т.е:
откуда:
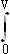 mvdv=mv2/2
mvdv=mv2/2Таким образом, тело массы m, движущееся со скоростью v, обладает кинетической энергией:
Кинетическая энергия – величина аддитивная. Так, энергия системы из n материальных точек равна сумме кинетических энергий этих материальных точек:
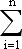 (mivi/2)
(mivi/2)Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому с обратным знаком, так как работа совершается за счет убыли потенциальной энергии системы:
Но δA=Fdr, тогда Fdr=-dП и потенциальную энергию системы можно найти как:
где C - постоянная интегрирования, то есть потенциальная энергия может быть определена с точностью до некоторой произвольной постоянной. Поэтому потенциальную энергию тела в каком-то положении полагают равной нулю, а энергию в других положениях отсчитывают относительно этого нулевого уровня (за нулевой уровень можно принять, например, уровень пола, уровень моря и т.д.).
Для консервативных сил:
Вектор, определяемый выражением (3.3), называется градиентом скаляра П.
Таким образом, выражение (3.2) показывает, что консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком.
Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна:
где h высота отсчитывается от уровня, для которого П0=0
Потенциальная энергия упругодеформированного тела (пружины):
Полная механическая энергия E системы – сумма кинетической и потенциальной энергий системы:
