Рассмотрим систему из n материальных точек массами m_i, движущихся со скоростями v_i( _i<< c). Пусть F'_i и F_i - равнодействующие внутренних и внешних консервативных сил, действующих на -ю точку, а - равнодействующая внешних неконсервативных сил, действующих на i-ю точку.

Уравнения второго закона Ньютона для этих точек:

За интервал dt точки совершают перемещения dr_i. Умножим каждое уравнение на соответствующее перемещение и учитывая, что dr_i=v_idt, получим:

Здесь 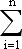m_i(v_idv_i)=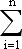d(m_iv_i²/2)=dT – приращение кинетической энергии системы;
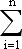(F'_i+F_i)dr_i=-dП - работа внутренних и внешних консервативных сил, взятая с обратным знаком, равная приращению потенциальной энергии системы;
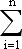f_idr_i - работа внешних неконсервативных сил, действующих на систему.

Итак, имеем:

Изменение полной механической энергии при переходе системы из состояния 1 в состояние 2 равно работе внешних неконсервативных сил:

Если внешние неконсервативные силы отсутствуют, то δA=0⇒d(T+П)=0, откуда:

т.е. полная механическая энергия системы сохраняется. Выражение (3.4) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

Механические системы, где действуют только консервативные силы (внутренние и внешние), называются консервативными системами. В консервативных системах полная механическая энергия остается постоянной, могут происходить лишь превращения кинетической энергии в потенциальную и наоборот. В частности, этот закон справедлив и для замкнутых консервативных систем.

В диссипативных системах механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) виды энергии. Этот процесс называется диссипацией (или рассеянием) энергии. Строго говоря, все системы в природе являются диссипативными.

В системе, где действуют также неконсервативные силы, полная механическая энергия не сохраняется, и закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.

Отметим, что закон сохранения энергии – фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.