Равномерное прямолинейное движение
Это такое движение, при котором материальная точка (тело) за любые равные промежутки времени проходит одинаковые отрезки по прямой. Уравнение скорости для такого движения имеет вид: 
v(t)=dr/dt=const (1.5)
Выразим отсюда элементарное перемещение dr=v*dt и, проинтегрировав по времени в пределах (0, t), получим уравнение радиуса-вектора:
Полагая для простоты, что вектор скорости направлен вдоль оси ОХ, можно записать уравнение (1.5) в скалярной форме:
vx(t)=dx/dt=const (1.5.a)
dx=vxdt (1.5.b)
Интегрируя выражение (1.5,б) по времени в пределах (0, t), получим уравнение пути:
S(t)=x-x0=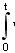 
vxdt=vxt
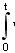vxdt=vxtЗдесь х0 – начальная координата движущейся точки. Отсюда уравнение координаты имеет вид:
x(t)=x0+vxt
Не следует забывать, что в зависимости от выбора положительного направления оси ОХ численное значение vx может быть как положительным, так и отрицательным.