Возьмем на плоскости две взаимно перпендикулярные прямые – две оси координат Ох и Оу с указанными на них положительными направлениями (рис.1). Прямые Ох и Оу называются координатными осями, точка их пересечения О – началом координат.

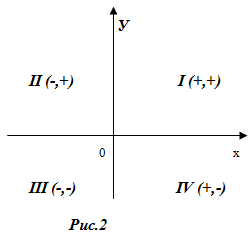
Координатные оси Ох, Оу с выбранной единицей масштаба называются декартовой прямоугольной (или прямоугольной) системой координат на плоскости.

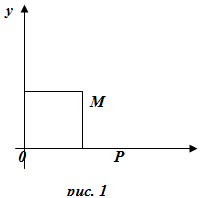
Произвольной точке М плоскости поставим в соответствие два числа:
абсциссу х, равную расстоянию от точки М до оси Оу, взятому со знаком «+», если М лежит правее Оу, и со знаком «-» ,если М лежит левее Оу; ординату у, равную расстоянию от точки М до оси Ох, взятому со знаком «+», если М лежит выше Ох, и со знаком «-», если М лежит ниже Ох. Абсцисса х и ордината у называются декартовыми прямоугольными координатами точки М(х;у).

Начало координат имеет координаты (0;0).
Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами (иногда их также называют координатными углами). Часть плоскости, заключенная между положительными полуосями Oх и Oу, называется первым квадрантом. Дальше нумерация квадрантов идет против часовой стрелки (рис. 2). Для всех точек I квадранта х>0, у>0; для точек I I квадранта х<0, у>0, в I I I квадранте х<0, у<0 и в IV квадранте х>0, у<0.